1. Физика
  2. Вывести формулу модуля всестороннего

Вывести формулу модуля всестороннего сжатия.

DasyaSay DasyaSay    1   04.03.2020 08:15    0

Ответы
ariana76 ariana76  27.08.2020 22:26

Рассмотрим сжатие куба.

Деформации его граней:

\varepsilon_x = \frac{\Delta x}{x}; \varepsilon_y= \frac{\Delta y}{y}; \varepsilon_z = \frac{\Delta z}{z}.

Каждая деформация складывается из относительного удлинения вдоль выбранной оси, равная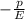 -\frac{p}{E} (p - давление, оказываемое на грань, E- модуль Юнга, "-" потому что сжатие) и деформаций, связанных с деформациями поперечных компонент, каждая из которых равна 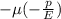-\mu(- \frac{p}{E}), где μ - коэффициент Пуассона.

Тогда:

\varepsilon_x =-\frac{p}{E} + \mu \frac{p}{E}+\mu \frac{p}{E} = -\frac{p}{E} (1-2\mu)

\varepsilon_y = -\frac{p}{E} (1-2\mu)

\varepsilon_z = -\frac{p}{E} (1-2\mu)

Суммарная деформация, выражается через модуль всестороннего сжатия K:

\frac{\Delta V}{V} = -\frac{p}{K},

С другой стороны:

\frac{\Delta V}{V} = \frac{\Delta x}{x} +\frac{\Delta y}{y} +\frac{\Delta z}{z} = \varepsilon_x +\varepsilon_y + \varepsilon_z = -3\frac{p}{E}(1-2\mu).

Отсюда:

K=\frac{E}{3(1-2\mu)}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
Lizo4ka20061 Lizo4ka20061  29.06.2019 05:10
Тело массой 600 г имеет объём 400см^3. какая необходима сила, чтобы удержать эту плиту в воде(дано, решение)...
andreikasuper andreikasuper  29.06.2019 05:10
N(азот) дельта m - ? eсвязи-? eудельная - ? , нужно решение...
cergei201088 cergei201088  15.07.2019 08:20
Всеть переменного тока с частотой 50 гц и напряжением 220 в включен конденсатор емкостью 4 мкф чему равна сила тока в цепи...
Kaka225 Kaka225  15.07.2019 08:20
Унас в 5 классе нам сказали выписать явления в природе не могу найти сказали вроде их 7 должно быть во примеры : механические магнитные световые продолжите...
lenusyamailru lenusyamailru  21.10.2020 14:35
При испарении вода охлаждается. Это объясняется тем, что воду покидают частицы… А) самые медленные В) самые быстрые Б) самые мелкие Г) самые крупные ​...
vomid5421 vomid5421  21.10.2020 14:35
Между двумя точечными зарядами +4∙10 -9 Кл и -5∙10 -9 Кл расстояние 60 см. Найдите напряженность в средней точке между зарядами....
аня2835 аня2835  21.10.2020 14:34
Одно обильное давление газа при постоянной температуре 10 К увеличилось в четыре раза. Какую работу выполняет газ?...
Dikiy2004 Dikiy2004  21.10.2020 14:34
Рассчитай высоту, на которой гравитационная сила, действующая на тело, будет в 7,7 раз меньше, чем на поверхности Земли. Радиус Земли принять равным 6400 км. ответ (округли до целого...
pankovakseniya pankovakseniya  06.07.2019 06:30
Средняя температура земли не меняется, несмотря на то, что земля постоянно получает энергию от солнца. так происходит из-за потери энергии через: а)теплопроводность б)излучение в)конвекцию...
Govnoegc Govnoegc  06.07.2019 06:30
Грузы массами м=2кг и м=1кг лежат на закреплённом несимметричном клине,углы при основании которго альфа=30 градусов и бета=45 градусов.нити нерастяжимы. трения нет. каково ускорение...

Популярные вопросы