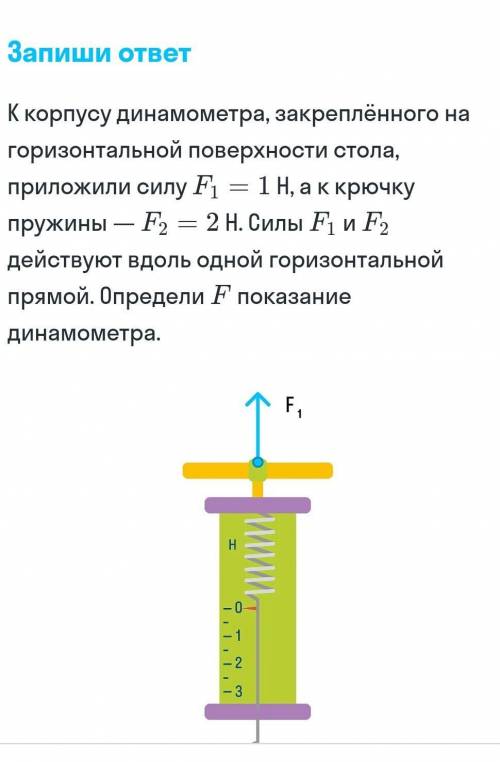
Все на фото, ответ выразить в ньютонах

На фото изображено тело, которое находится на наклонной плоскости под углом θ к горизонту. Тело покоится на плоскости и не движется. Нас интересует сила F, которая действует параллельно плоскости и уравновешивает сумму всех сил, направленных вдоль наклонной плоскости.

Для решения этой задачи нам понадобятся знания о силе тяжести, перпендикулярной плоскости, и о силе нормальной реакции, направленной вдоль плоскости.

Для начала давайте разложим силу тяжести на две составляющие: одна будет направлена перпендикулярно плоскости, а другая - параллельно плоскости. Перпендикулярная составляющая равна m * g * cos(θ), где m - масса тела, g - ускорение свободного падения, а θ - угол наклона плоскости. Параллельная составляющая равна m * g * sin(θ).

Теперь давайте рассмотрим силы, действующие вдоль плоскости. К ним относятся сила трения Fтр и сила нормальной реакции n. Согласно условию задачи, тело покоится, поэтому сумма этих двух сил равна нулю: Fтр + n = 0. Сила трения равна коэффициенту трения μ, умноженному на силу нормальной реакции: Fтр = μ * n.

После этого мы можем записать уравнение равновесия сил вдоль плоскости: F - Fтр = 0, где F - искомая сила, направленная параллельно плоскости.

Теперь выразим силу трения через силу нормальной реакции, используя уравнение Fтр = μ * n: F - μ * n = 0.

Однако мы пока не знаем силу нормальной реакции, поэтому продолжим решение, используя геометрические соображения. Поскольку тело покоится на наклонной плоскости, сила нормальной реакции будет равна проекции силы тяжести на перпендикуляр к плоскости. То есть, n = m * g * cos(θ).

Теперь мы можем подставить это значение силы нормальной реакции в уравнение F - μ * n = 0: F - μ * (m * g * cos(θ)) = 0.

И, наконец, выразим искомую силу F: F = μ * (m * g * cos(θ)).

Ответ: искомая сила F, размер которой выражен в ньютонах, равна μ * (m * g * cos(θ)).

Для получения числового результата необходимо знать значения массы тела (m), ускорения свободного падения (g) и коэффициента трения (μ), а также угол наклона плоскости (θ). Подставив эти значения в формулу, можно вычислить искомую силу F.