Все ! маятник длиной 3 м выводят из положения равновесия и отпускают. определи, сколько раз за 2,5 мин кинетическая энергия маятника достигнет максимального значения. при расчетах прими π=3,14, g=9,8 м/с². ответ: раз

Ответы

ЕВБ 10.10.2020 00:46

Кинетическая энергия математического маятника достигает максимума в нижней точке 1 раз за период колебания.

Период колебания маятника: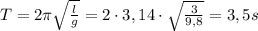 $T = 2 \pi \sqrt{\frac{l}{g}} = 2 \cdot 3,14 \cdot \sqrt{\frac{3}{9,8}} = 3,5s$

Тогда ответ: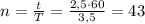 $n = \frac{t}{T} = \frac{2,5 \cdot 60}{3,5} = 43$ раза.

ПОКАЗАТЬ ОТВЕТЫ

glushcovapolia 24.01.2024 13:14

Хорошо, давайте разберем данную задачу шаг за шагом.

Для начала, вспомним основные понятия, которые пригодятся для решения задачи.

Маятник - это тело, которое движется по закону гармонического колебания. В данной задаче мы имеем дело с простым математическим маятником, который представляет собой невесомый стержень длиной 3 м, с одним концом закрепленным и вращающимся вокруг оси, а другим концом находится груз.

Для того чтобы рассчитать количество раз, когда кинетическая энергия маятника достигнет максимального значения, нужно знать, как меняется кинетическая энергия маятника во времени.

Кинетическая энергия маятника выражается формулой:
K = (m * v²) / 2,

где K - кинетическая энергия, m - масса груза на конце маятника, v - скорость груза.

Суть задачи заключается в том, чтобы определить изменения скорости груза во времени и найти моменты времени, когда скорость достигает максимального значения.

Для этого воспользуемся законами гармонического колебания и известными параметрами маятника.

Период колебаний(T) математического маятника можно вычислить по формуле:
T = 2π * √(l / g),

где l - длина маятника, g - ускорение свободного падения.

В данной задаче длина маятника l = 3 м, а ускорение свободного падения g = 9,8 м/с².

T = 2π * √(3 / 9,8) = 2π * √(0,306) ≈ 2π * 0,553 ≈ 3,48 сек.

Теперь, зная период колебаний маятника, найдем количество колебаний, которые происходят в течение 2,5 мин (1 мин = 60 сек).

Количество колебаний (n) можно вычислить по формуле:
n = (время) / (период колебаний) = (2,5 * 60) / 3,48 ≈ 42,76,

округлим до ближайшего целого числа, получаем n ≈ 43.

Значит, за 2,5 мин кинетическая энергия маятника достигнет максимального значения 43 раза.

Ответ: раз.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Физика