Впоследнюю секунду свободного падения тело преодолело 5/9 всего пути. определите высоту, с которой падало тело. считайте, что g = 10 м/с²
Ответы
Найдем расстояние, которое преодолевает падающее тело за t-ую секунду: 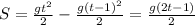 ; В данном случае, t-aя секунда - это последняя секунда. То есть все падение заняло t секунд. Пусть весь путь равен H, тогда имеем:
; В данном случае, t-aя секунда - это последняя секунда. То есть все падение заняло t секунд. Пусть весь путь равен H, тогда имеем: 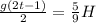 , откуда
, откуда 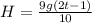 ; С другой стороны
; С другой стороны 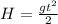 ; Приравняем оба найденных значения H:
; Приравняем оба найденных значения H: 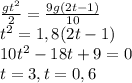 ;
; 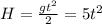 ; Отсюда высота равна 45 метров, так как решение t=0,6 с не имеет смысла согласно формулировке условия задачи. ответ: 45 метров
; Отсюда высота равна 45 метров, так как решение t=0,6 с не имеет смысла согласно формулировке условия задачи. ответ: 45 метров
ПОКАЗАТЬ ОТВЕТЫ
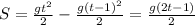 ; В данном случае, t-aя секунда - это последняя секунда. То есть все падение заняло t секунд. Пусть весь путь равен H, тогда имеем:
; В данном случае, t-aя секунда - это последняя секунда. То есть все падение заняло t секунд. Пусть весь путь равен H, тогда имеем: 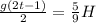 , откуда
, откуда 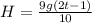 ; С другой стороны
; С другой стороны 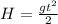 ; Приравняем оба найденных значения H:
; Приравняем оба найденных значения H: 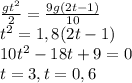 ;
; 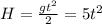 ; Отсюда высота равна 45 метров, так как решение t=0,6 с не имеет смысла согласно формулировке условия задачи. ответ: 45 метров
; Отсюда высота равна 45 метров, так как решение t=0,6 с не имеет смысла согласно формулировке условия задачи. ответ: 45 метров
Другие вопросы по теме Физика
Популярные вопросы
- по 5 примеров на темы: * удвоенная согласная в корне; * непроизносимая...
3 - Счем и почему сравнивается битва в слово о полку игореве ?...
2 - Что является основной единицей времени?...
3 - Выпишите противоположные по значению словосочетания - всходить на востоке,...
1 - Описание свойств алюминия (цвет, запах,растворимость, температура кипения,...
1 - Напишите сочинение(рассуждение) на тему культура речи. только не с интернета...
1 - Определите массу молекулярного водорода(h2) занимающего объём 1 м^3 при...
2 - Какая дробь больше: 1989/1990 и 1999/2000...
3 - Перечислите наиболее важные наставления князя и прокомментируйте их....
2 - Вчём различия между учёным и следователем...
2