Вопрос с исчерпывающими подробностями изложен в приложенном документе.

кратко, проблема состоит в применении закона схранения энергии к точечному заряду и совокупно нейтральному проводнику в его поле. используя элементаный анализ, применяемый классической электростатикой, мы приходим к парадоксальному уравнению:

$w_o = w' + \frac{mv^2}{2}$ , в котором значения потенциальных энергий, соответствующие разным последовательным состояниям, должны оказаться равными $w_o = w'$ , в соответствии с элеметарной теорией проводников. но и скорость проводника при этом оказывается отличной от нуля, что легко проверить в эксперименте, т.е. $v^2\ \textgreater \ 0$ . откуда и приходим к парадоксу:

$0 = \frac{mv^2}{2} \ \textgreater \ 0$ ;

ситуация в реальности усугубляется ещё и тем, что в проводнике происходит омическое нагревание, и часть энергии излучается:

$w_o = w' + \frac{mv^2}{2} + \delta q^o_r + \delta w_{ray}$ ;

где:

$w_o = w'=0$ – строго! (эквипотенциальность проводника)
$\frac{mv^2}{2} \ \textgreater \ 0$ – строго! (ускорение из-за притяжения)
$\delta q_r^o \ \textgreater \ 0$ – строго! (омическое нагревание)
$\delta w_{ray} \ \textgreater \ 0$ – строго! (излучение)

может быть проводник охлаждается, вследствие каких-то неучтённых квантовых эффектов на его поверхности? может быть он поглощает больше электромагнитной энергии, чем излучает? или причина в чём-то ещё?

решение как раз должно разрешить парадокс и устранить противоречия в уравнениях и неравенствах. в силу высокой сложности выражения распределения зарядов на проводнике даже элементарной формы, решение подразумевается, конечно же, качественное, с точностью до знаков в неравенствах.

Ответы

maksimesaulav46 05.08.2020 08:17

С рассмотрением движения всё сложно, придётся рассматривать какие-нибудь запаздывающие потенциалы, ещё что-нибудь.

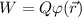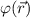Пусть скорости настолько малы, что можно применять электростатику. Выберем систему координат, в которой проводник покоится. Полная энергия системы точечный заряд + проводник равна $W=Q\varphi(\vec r)$ , где $\varphi(\vec r)$ – потенциал, создаваемый проводником, в точке, в которой находится заряд Q; кинетическая энергия мала. 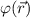$\varphi(\vec r)$ зависит от положения заряда.

Упрощенная модель: задача одномерная; Q расположен в точке x = L; на поверхности проводника возникают два заряда -q и q в точках x = r, x = -r, причём r << L, r и q не зависят от L.

Потенциальная энергия (в системе СГС):

$W=Q\left(-\dfrac q{L-r}+\dfrac q{L+r}\right)=\dfrac{qQ}{L}\left(-\left(1+\dfrac rL\right)+\left(1-\dfrac rL\right)\right)=-\dfrac{2rqQ}{L^2}$

Здесь видно, что потенциальная энергия системы уменьшается при уменьшении L. Уменьшение этой энергии и уйдет на увеличение кинетической энергии и излучение.

Омические потери тут немного не к месту: если есть омические потери, то проводник не идеальный, и поверхность, строго говоря, не эквипотенциальная.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Физика