Во сколько раз изменится (увеличится или уменьшится) период колебаний маятника при перемещение его с земли на луну? сила тяготения

Question

Физика: Во сколько раз изменится (увеличится или уменьшится) период колебаний маятника при перемещение его с земли на луну? сила тяготения на поверхности луны в 6 раз меньше, чем на земле.

Samsas · Answer

Период колебания математического маятника вычисляется по формуле:

$T = 2 \pi \sqrt{\frac{L}{g}}$ , где L - длина маятника.

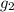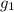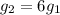Ускорение свободного падения на Земле g_2 в 6 раз больше ускорения свободного падения на Луне g_1 : g_2 = 6 g_1 .

Отношение периодов колебания маятника на Луне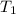 T_1 и на Земле 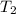T_2 равно: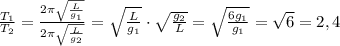 $\frac{T_1}{T_2} = \frac{2 \pi \sqrt{\frac{L}{g_1}}} {2 \pi \sqrt{\frac{L}{g_2}}} = \sqrt{\frac{L}{g_1}} \cdot \sqrt{\frac{g_2}{L}} = \sqrt{\frac{6g_1}{g_1}}=\sqrt{6}=2,4$

ответ: период колебания математического маятника на Луне в 2,4 раза больше, чем на период колебания этого маятника на Земле.

Популярные вопросы