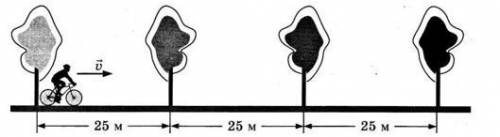
Вдоль прямой дороги на равном расстоянии высажены деревья. Велосипе­дист начинает двигаться по дороге с постоянной скоростью 5 м/с. Используя данные рисунка, выберите из предложенного перечня два вер­ных утверждения.

Укажите их номера.

1) За 20 с движения велосипедист проедет мимо пяти деревьев.

2) На преодоление расстояния между соседними деревьями велосипедист тратит 5 с.

3) На преодоление расстояния между соседними деревьями велосипедист тратит 50 с.

4) Мимо соседних деревьев велосипедист проезжает за разное время.

5) На преодоление расстояния между тремя деревьями велосипедист тра­тит 15 с.

Чтобы ответить на данный вопрос, давайте разберем каждое утверждение по порядку и рассмотрим их верность.

1) За 20 с движения велосипедист проедет мимо пяти деревьев.
Для проверки этого утверждения мы должны выяснить, сколько времени требуется велосипедисту, чтобы пройти одно дерево. По условию задачи известно, что деревья высажены на равном расстоянии друг от друга и велосипедист двигается с постоянной скоростью 5 м/с. Если обозначим количество деревьев как "n", то расстояние между деревьями будет "n-1". За время t велосипедист пройдет расстояние vt, где v - скорость, t - время. Таким образом, расстояние между соседними деревьями равно vt, а общее расстояние, которое пройдет велосипедист во время прохождения всех деревьев, будет равно (n-1)vt.
Из условия задачи известно, что за 20 секунд велосипедист проезжает все деревья, поэтому можно составить уравнение:
(n-1)vt = 20
5(n-1) = 20
5n - 5 = 20
5n = 25
n = 5
Таким образом, при условии прохождения всех деревьев за 20 секунд, можно сделать вывод, что велосипедист проедет мимо пяти деревьев. Утверждение 1 верно.

2) На преодоление расстояния между соседними деревьями велосипедист тратит 5 секунд.
Для проверки этого утверждения мы можем использовать выведенные ранее значения. Количество деревьев равно 5, а время прохождения одного дерева равно 20 секунд. Если мы разделим общее время на количество деревьев, то получим:
20 / 5 = 4 секунды.
Таким образом, на преодоление расстояния между соседними деревьями велосипедист тратит 4 секунды, а не 5. Утверждение 2 неверно.

3) На преодоление расстояния между соседними деревьями велосипедист тратит 50 секунд.
Аналогично предыдущему утверждению, мы можем использовать выведенные ранее значения. Количество деревьев равно 5, а время прохождения одного дерева равно 20 секунд. Если мы разделим общее время на количество деревьев, то получим:
20 / 5 = 4 секунды.
Таким образом, на преодоление расстояния между соседними деревьями велосипедист тратит 4 секунды, а не 50. Утверждение 3 неверно.

4) Мимо соседних деревьев велосипедист проезжает за разное время.
Из предыдущего рассуждения мы можем сделать вывод, что велосипедист проезжает мимо каждого дерева за одинаковое количество времени, так как расстояние между деревьями одинаковое. Поэтому утверждение 4 неверно.

5) На преодоление расстояния между тремя деревьями велосипедист тратит 15 секунд.
Так как количество деревьев равно 5 и расстояние между соседними деревьями одинаковое, мы можем использовать ранее выведенное значение времени на преодоление расстояния между соседними деревьями - 4 секунды. Если велосипедист проходит расстояние между тремя деревьями, то это значит, что он проходит расстояние между двумя соседними деревьями дважды. Следовательно, время на преодоление расстояния между тремя деревьями будет равно:
2 * 4 = 8 секунд.
Таким образом, на преодоление расстояния между тремя деревьями велосипедист тратит 8 секунд, а не 15. Утверждение 5 неверно.

В итоге, только первое утверждение является верным, поэтому мы выбираем номер 1.