Вариант ! При средней кинетической энергии E поступательного движения молекул идеального газа температура газа составляет (t=?)Определите значение величины, обозначенной *t. 0 C Как изменится абсолютная температура газа при изменении средней кинетической энергии поступательного движения молекул в 4 раза?
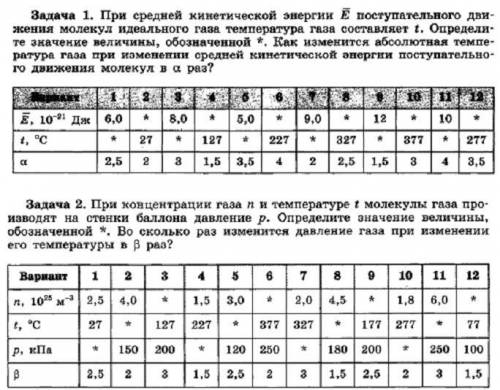
Ответы
Для того чтобы решить эту задачу, нам необходимо применить формулу для кинетической энергии поступательного движения молекул идеального газа, а также воспользоваться законом Гей-Люссака.
1. Начнем с формулы для кинетической энергии поступательного движения молекул идеального газа:
E = (3/2) * k * T,
где E - средняя кинетическая энергия поступательного движения молекул газа,
k - постоянная Больцмана (k ≈ 1.38 * 10^-23 Дж/К),
T - абсолютная температура газа.
2. Теперь введем новую среднюю кинетическую энергию, обозначим ее как E1. По условию задачи, E1 = 4E.
3. Подставим E1 в формулу для кинетической энергии идеального газа:
E1 = (3/2) * k * T1,
где T1 - новая абсолютная температура газа.
4. Теперь можно выразить T1 через T и E:
(3/2) * k * T1 = E1,
(3/2) * k * T1 = 4E,
T1 = (4E) / ((3/2) * k),
T1 = (8E) / (3k).
5. В данной задаче мы хотим узнать, как изменится абсолютная температура газа при увеличении средней кинетической энергии в 4 раза. То есть, мы хотим выразить T1 через T:
T1 = tT, где t - некоторый коэффициент.
6. Подставим это выражение для T1 в предыдущее уравнение:
tT = (8E) / (3k),
t = (8E) / (3kT).
7. Окончательный ответ:
Значение величины, обозначенной *t, равно t = (8E) / (3kT).
Таким образом, чтобы найти значение величины *t, нам необходимо знать среднюю кинетическую энергию поступательного движения молекул газа (E), постоянную Больцмана (k) и абсолютную температуру газа (T). Затем мы можем использовать формулу t = (8E) / (3kT) для расчета этой величины.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
Популярные вопросы
- Прочитай текст и Выполни задания Какая бывает роса на траве Когда в солнечное...
1 - 321. Перепишите, расставляя знаки препинания. Объяснитеих употребление. Вставьте...
1 - сор по матеше Суммативное оценивание по математике No 4 1. На координатной...
3 - Сөйлемнің жалғасын тауып, толықтырып жаз. Осы кітапханада оқыған білімге ұмтылған...
2 - 7. В пятиугольнике стороны AB и DE равны 2 см, BC и EA в 3 раза больше AB,...
1 - Сор плз Работа с картой – объясни закономерность распространения природного...
1 - Поясніть метафору (павутинка) , на якій побудована новела Р. Акутагави? Нужна...
1 - Истынкт поверненя до дому це...
2 - Укажите, какую информацию текста можно выделить как второстепенную? Почему?...
1 - Вариант 1. Часть 1.Выберите один верный ответ, запишите его буквой.1.Термины...
1