1. Физика
  2. Вал вращается согласно

Вал вращается согласно уравнению: φ=1,1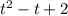t^{2} -t+2, рад.Определить угловую скорость в момент времени t=1с. Сколько оборотов сделает вал за 2 минуты?

polinavorkuta polinavorkuta    1   02.07.2020 13:32    3

Ответы
dkdjdhhs dkdjdhhs  15.10.2020 15:10

1,2 рад/с

2502 оборота

Объяснение:

Угловая скорость вращения вала равна первой производной угла поворота по времени

\omega (t)=\frac{d\phi (t)}{dt}=2.2t-1

Угловая скорость в указанный момент времени

\omega (1)=2.2*1-1=1.2 рад/с

Здесь целесообразно разбить весь промежуток времени на два, в пределах которых вал вращался в разные стороны. Для интервала времен 0<t<1/2.2 - вал вращается в одну сторону и поворачивается на угол φ(1/2,2)-φ(0)=-0.23 рад (можно не учитывать).

Второй, основной промежуток времени скорость вала положительна и он примерно поворачивается на угол

\phi (120)=1.1*120^2-120+2=15722 рад

Разделив это число на 2π найдем число оборотов

N=\frac{\phi }{2\pi } =\frac{15722}{2\pi } =2502 оборота.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
Ипак44 Ипак44  27.09.2019 04:20
На земле свинцовые пластины сложены в груду, высота которой равна 1,7 м. какое давление оказывает груда пластин на землю (g≈10м/с2) ? ответ: давление равно па, или кпа....
kononovadm kononovadm  27.09.2019 04:30
Відчинивши вікно , хлопчик спочатку поставив палаючу свічку на підвіконня , а потім підніс її догори у який бік і чому відхилялося полум я свічки в обох випадках , якщо...
КатяХалина КатяХалина  27.09.2019 04:30
Под действием гири весом 7 н длина пружины динамометра равна 8 см, а при подвешивании гири весом 3 н длина пружины динамометра равна 6 см. найди длину пружины динамометра...
S1mplendnnd S1mplendnnd  27.09.2019 04:30
Найти спин (spin) тензорных мезонов. (h-постоянная планка) a) h/2 b) h/4п c) h/п d) 0. здесь п-чило пи постоянная равная 3. ответьте !...
gea99 gea99  27.09.2019 04:30
Вес куска сплава в воде (ρ=1000 кг/м3) равен 4,8 н, а в керосине (ρ=800 кг/м3) равен 5,5 н. определите плотность сплава (кг/м3)....
Алексей211177 Алексей211177  27.09.2019 04:30
Определить энергию фотона, соответствующего kα – линии ( λ= 0,7 å) в спектре характеристического рентгеновского излучения молибдена....
m1a2s3h4a51999 m1a2s3h4a51999  15.03.2019 03:40
Дано уравнение движения тела: х=-5t+t^2 заполните таблицу: 1.начальная координата 2.начальная скорость 3.ускорение 4.уравнение скорости 5.уравнение перемещения 6.характер...
vavavvavavavava vavavvavavavava  15.03.2019 02:53
Дно ящика массой 250кг имеет площадь 0,1м квадратных вычислить давление...
А22222222 А22222222  15.03.2019 03:50
Сколько теплоты требуется для нагревания свинцовой детали массой 200 г на 70 с...
Кисаааа123 Кисаааа123  15.03.2019 02:32
Как найти реакции опор, они тут есть, но решение нужно самому найти, чтобы ответ такой же получился?...

Популярные вопросы