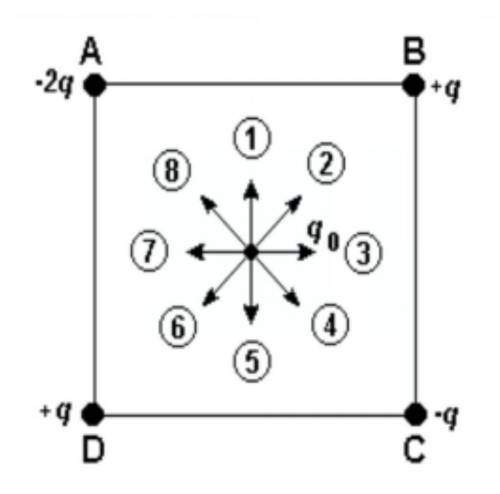
В вершинах квадрата находятся точечные заряды, причем заряд, находящийся в вершине A, в 2 раза больше по модулю, чем заряды в вершинах B, C и D (см. рисунок). В центр квадрата помещен точечный положительный заряд q0. Какой из пронумерованных на рисунке векторов совпадает с направлением вектора результирующей силы, действующей на заряд q0 со стороны других зарядов?

Чтобы определить направление вектора результирующей силы на заряд q0, мы можем использовать закон Кулона, который гласит, что сила, действующая между двумя точечными зарядами, прямо пропорциональна их зарядам и обратно пропорциональна квадрату расстояния между ними.

В данной задаче мы имеем несколько зарядов: zA (заряд в вершине A), zB, zC и zD (заряды в вершинах B, C и D). Пусть нас будет интересовать только направление вектора результирующей силы, поэтому мы можем произвольно выбрать заряд q0 равным 1.

Из условия задачи мы знаем, что заряд в вершине A в 2 раза больше по модулю, чем заряды в вершинах B, C и D. Предположим, что заряды в вершинах B, C и D равны по модулю, пусть они будут равны -1.

Теперь мы можем использовать закон Кулона для определения модуля силы, действующей на заряд q0 со стороны каждого из зарядов в вершинах. Расстояние между зарядами в вершинах и зарядом q0 равно диагонали квадрата, которая равна √2.

Силы, действующие на заряд q0 со стороны зарядов zA, zB, zC и zD, соответственно, равны:
F = k * (|zA| * |q0|) / r^2 = k * (2 * 1) / (√2)^2 = k / 2,
F = k * (|zB| * |q0|) / r^2 = k * (1 * 1) / (√2)^2 = k / 2,
F = k * (|zC| * |q0|) / r^2 = k * (1 * 1) / (√2)^2 = k / 2,
F = k * (|zD| * |q0|) / r^2 = k * (1 * 1) / (√2)^2 = k / 2,

где k - постоянная Кулона, которая равна 1 / (4πε0), где ε0 - электрическая постоянная.

Таким образом, модуль силы, действующей на заряд q0, со стороны каждого из зарядов в вершинах одинаков и равен k / 2.

Зная, что сила - векторная величина, то вектор результирующей силы будет совпадать с направлением силы, действующей на заряд q0 со стороны зарядов в вершинах. Таким образом, вектор результирующей силы будет совпадать с любым из векторов, направленных от зарядов в вершинах к центру квадрата (то есть с векторами, указанными на рисунке как 1, 2, 3 или 4).