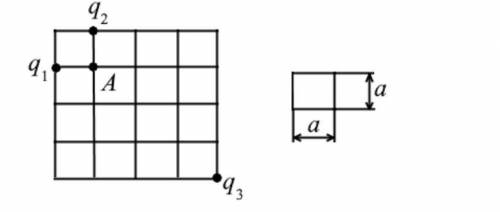
В узлах решетки находятся точечные заряды q1 =q, q2 =q и q3 =−2q. В узлах решетки находятся точечные заряды q1 =q, q2 =q и q3 =−2q. Найти потенциал электрического поля в точке . (Одна ячейка имеет форму квадрата со стороной .)

Для решения этой задачи нам понадобятся знания о законе Кулона и потенциале электрического поля.

Закон Кулона гласит, что сила взаимодействия между двумя точечными зарядами пропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния между ними. То есть, для нас важно знать значения зарядов и расстояния между ними.

Потенциал электрического поля в точке можно найти с использованием формулы:
V = k * (q1/r1 + q2/r2 + q3/r3),
где V - потенциал электрического поля в точке, k - постоянная Кулона (9 * 10^9 Н м^2/Кл^2), q1, q2, q3 - заряды, r1, r2, r3 - расстояния от зарядов до точки.

Давайте применим эту формулу для данной задачи.
Заряды в узлах решетки - q1 = q, q2 = q и q3 = -2q.

Разберемся с расстояниями:
1) Расстояние от точки до заряда q1.
Так как каждая ячейка решетки имеет форму квадрата, расстояние до заряда q1 будет равно длине стороны квадрата, то есть a.

2) Расстояние от точки до заряда q2.
Аналогично, расстояние до заряда q2 также будет равно длине стороны квадрата a.

3) Расстояние от точки до заряда q3.
Согласно заданию, в узлах решетки расположены заряды по диагонали относительно точки. Расстояние от точки до заряда q3 будет равно длине диагонали квадрата, что равняется sqrt(2) * a.

Теперь, подставим все значения в формулу и произведем расчет:
V = k * (q1/r1 + q2/r2 + q3/r3)
V = (9 * 10^9 Н м^2/Кл^2) * (q/a + q/a + (-2q)/(sqrt(2) * a))

Упрощаем выражение:
V = (9 * 10^9 Н м^2/Кл^2) * (2q/a - 2q/a*sqrt(2))
V = (9 * 10^9 Н м^2/Кл^2) * (2q/a * (1 - 1/sqrt(2)))
V = (9 * 10^9 Н м^2/Кл^2) * (2q/a * (sqrt(2) - 1) / sqrt(2))

Таким образом, мы получили выражение для потенциала электрического поля в данной задаче. В ответе можно оставить его в таком виде. Если нужно получить численное значение, необходимо знать значения заряда q и длины стороны квадрата a, чтобы подставить их в выражение и произвести расчет.