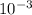
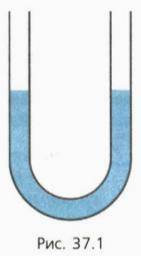
В U-образной трубке с одинаковыми коленами, площадью поперечного сечения каждое, находится вода (рис. 37.1). В левое колено наливают 0,1 кг керосина. а) Изобразите на чертеже положение жидкостей в коленах трубки.
б) Чему равна высота столба керосина?
в) Чему равно давление жидкостей на уровне границы раздела жидкостей?
г) Чему равна высота столба воды в правом колене над уровнем раздела жидкостей?
д) Насколько поднялся уровень воды в правом колене по сравнению с начальным положением?
Подсказка. В правом колене уровень воды поднялся настолько же, насколько он опустился в левом колене (поскольку объем воды не изменился).

a) На чертеже нужно изобразить положение жидкостей в коленах трубки. В левом колене находится керосин, а в правом колене – вода. Оба колена имеют одинаковую площадь поперечного сечения.

b) Высоту столба керосина можно определить, зная его массу и плотность. Масса керосина равна 0,1 кг. Плотность керосина обычно составляет примерно 800 кг/м^3. Таким образом, объем керосина равен массе керосина, поделенной на его плотность:

V_керосина = m_керосина / ρ_керосина = 0,1 кг / (800 кг/м^3) = 0,000125 м^3

Так как площадь поперечного сечения каждого колена равна 10^-3 м^2, то высота столба керосина равна объему керосина, поделенному на площадь поперечного сечения колена:

h_керосина = V_керосина / A_колена = 0,000125 м^3 / (10^-3 м^2) = 0,125 м

Таким образом, высота столба керосина составляет 0,125 метра.

в) Давление жидкости на уровне границы раздела жидкостей можно определить, используя формулу давления P = ρgh. Здесь ρ – плотность жидкости, g – ускорение свободного падения, h – высота столба жидкости.

Находящаяся в левом колене керосин и находящаяся в правом колене вода оказывают равенство давлений на границе раздела жидкостей.

Таким образом, давление жидкостей на уровне границы раздела жидкостей одинаково и равно P = P_керосина = P_воды.

г) Высоту столба воды в правом колене над уровнем раздела жидкостей можно определить, учитывая, что уровень воды в правом колене поднялся настолько же, насколько он опустился в левом колене. Другими словами, высота столба воды в правом колене равна высоте столба керосина.

h_воды_правое = h_керосина = 0,125 м

д) Уровень воды в правом колене поднялся на то же расстояние, на сколько опустился уровень воды в левом колене. Поскольку давление на границе раздела жидкостей одинаково, а плотность воды и площадь поперечного сечения колена не изменились, можно сделать вывод, что объем воды остался таким же.

Таким образом, уровень воды в правом колене поднялся на то же расстояние, на сколько опустился уровень воды в левом колене.