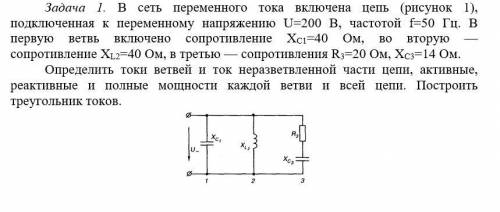
В сеть переменного тока включена цепь (рисунок 1), подключенная к переменному напряжению U=200 В, частотой f=50 Гц. В первую ветвь включено сопротивление ХC1=40 Ом, во вторую — сопротивление XL2=40 Ом, в третью — сопротивления R3=20 Ом, ХC3=14 Ом. Определить токи ветвей и ток неразветвленной части цепи, активные, реактивные и полные мощности каждой ветви и всей цепи. Построить треугольник токов.
3 ветвь считать не нужно

Добрый день! Давайте разберемся с данным вопросом. Для начала, нам нужно определить токи ветвей и ток неразветвленной части цепи.

1. Ток в первой ветви (I1):
Используем закон Ома: U = I * Z, где U - напряжение, I - ток, Z - импеданс.
Импеданс для резистора (XC1) равен его сопротивлению: ZC1 = XC1 = 40 Ом.
Таким образом, I1 = U / ZC1 = 200 В / 40 Ом = 5 А.

2. Ток во второй ветви (I2):
Импеданс для катушки индуктивности (XL2) можно рассчитать по формуле XL = ωL, где ω - угловая частота, L - индуктивность.
Угловая частота (ω) выражается через частоту (f) следующим образом: ω = 2πf.
Значит, ω = 2 * π * 50 Гц ≈ 314 рад/с.
Используя данное значение, импеданс для катушки индуктивности (Xl2) равен XL2 = ωL2 = 314 рад/с * 40 Ом = 12560 Ом.
Таким образом, I2 = U / XL2 = 200 В / 12560 Ом ≈ 0.016 А (или около 16 мА).

3. Ток в третьей ветви (I3):
Импеданс для третьей ветви включает в себя сопротивление (R3) и реактивное сопротивление (Xc3).
Импеданс для параллельного подключения резистора и катушки индуктивности может быть рассчитан по формуле: Z = sqrt(R^2 + X^2), где R - сопротивление, X - реактивное сопротивление.
Здесь R3 = 20 Ом, Xc3 = 14 Ом.
Подставим данные в формулу: Z3 = sqrt((R3^2) + (Xc3^2)) = sqrt((20^2) + (14^2)) ≈ 24.5 Ом.
Таким образом, I3 = U / Z3 = 200 В / 24.5 Ом ≈ 8.16 А.

4. Ток неразветвленной части цепи (Iн):
Так как цепь разветвляется на три ветви, ток неразветвленной части цепи равен сумме токов во всех ветвях: Iн = I1 + I2 + I3 = 5 А + 0.016 А + 8.16 А ≈ 13.17 А (или около 13.17 А).

Теперь давайте рассчитаем активные, реактивные и полные мощности каждой ветви и всей цепи.

1. Мощность в первой ветви (P1):
Активная мощность (P) может быть рассчитана по формуле: P = I^2 * R, где I - ток, R - сопротивление.
Таким образом, P1 = (I1^2) * R1 = (5 А)^2 * 40 Ом = 1000 Вт.

Реактивная мощность (Q) выражается по формуле: Q = I^2 * X, где X - импеданс.
Поскольку реактивное сопротивление (XC) является индуктивным, реактивная мощность будет положительной.
Q1 = (I1^2) * XC1 = (5 А)^2 * 40 Ом = 1000 ВАр (вольт-ампер реактивных).

Полная мощность (S) выражается по формуле: S = sqrt(P^2 + Q^2).
S1 = sqrt((1000 Вт)^2 + (1000 ВАр)^2) ≈ 1414 ВА (вольт-ампер).

2. Мощность во второй ветви (P2, Q2, S2):
Рассчет проводится аналогичным образом:
P2 = (I2^2) * Xl2 ≈ (0.016 А)^2 * 12560 Ом ≈ 3.2 Вт.
Q2 = (I2^2) * Xl2 ≈ (0.016 А)^2 * 12560 Ом ≈ 3.2 ВАр (вольт-ампер реактивных).
S2 = sqrt((3.2 Вт)^2 + (3.2 ВАр)^2) ≈ 4.5 ВА (вольт-ампер).

3. Мощность в третьей ветви (P3, Q3, S3):
Рассчет проводится аналогичным образом:
P3 = (I3^2) * R3 ≈ (8.16 А)^2 * 20 Ом ≈ 1340 Вт.
Q3 = (I3^2) * Xc3 ≈ (8.16 А)^2 * 14 Ом ≈ 929 ВАр (вольт-ампер реактивных).
S3 = sqrt((1340 Вт)^2 + (929 ВАр)^2) ≈ 1616 ВА (вольт-ампер).

4. Мощность неразветвленной части цепи (Pн, Qн, Sн):
Рассчет проводится аналогичным образом:
Pн = (Iн^2) * R1 ≈ (13.17 А)^2 * 40 Ом ≈ 7045 Вт.
Qн = (Iн^2) * XC1 ≈ (13.17 А)^2 * 40 Ом ≈ 7045 ВАр (вольт-ампер реактивных).
Sн = sqrt((7045 Вт)^2 + (7045 ВАр)^2) ≈ 9950 ВА (вольт-ампер).

Теперь построим треугольник токов.
Примечание: для удобства построения, уменьшим значения токов в 100 раз (т.е. делим все значения токов на 100).
Треугольник строится по принципу векторной суммы токов в каждой ветви.

1. ВОЛНОВЫЙ УГОЛ (∠):
Для каждого тока в ветви можно найти его волновой угол (фазу) с помощью арктангенса отношения реактивного сопротивления к активному сопротивлению.
Например, для первой ветви: ∠I1 = arctan(XC1 / R1) = arctan(40 Ом / 40 Ом) = 45 градусов.

2. ТРЕУГОЛЬНИК ТОКОВ:
- Рисунок треугольника токов
- Первая ветвь: от начала координат проводим вектор I1 в направлении, соответствующему волновому углу ∠I1 и с длиной, пропорциональной значению тока I1.
- Вторая ветвь: от конца первой ветви проводим вектор I2 в направлении, соответствующему волновому углу ∠I2 и с длиной, пропорциональной значению тока I2.
- Третья ветвь: от конца второй ветви проводим вектор I3 в направлении, соответствующему волновому углу ∠I3 и с длиной, пропорциональной значению тока I3.

Таким образом, мы получаем треугольник токов, где длина каждой стороны пропорциональна значению тока в соответствующей ветви, и углы между векторами равны их волновым углам.

Это весь ответ на данный вопрос. Если у вас возникли какие-либо вопросы или нужны дополнительные пояснения, пожалуйста, не стесняйтесь задавать их. Я всегда готов помочь!