В однородном магнитном поле в плоскости, перпендикулярной к линиям индукции, расположены два проводника 1 и 2 одинаковой длины l с одинаковыми токами I. Найдите отношение F1/F2 - модулей сил Ампера, действующих на эти проводники ? Желательно с пояснением
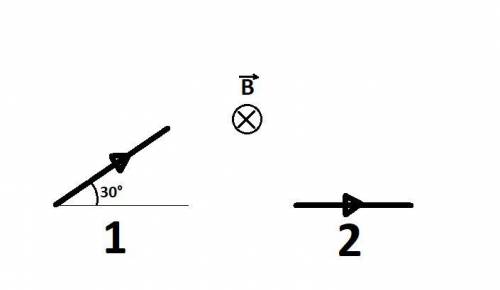
Другие вопросы по теме Физика
Популярные вопросы
- Интересные сведения о спортсменах у которых развиты сила ловкость...
3 - Найдите число ,если 7/8 его равны 91...
1 - На рисунке abcd-прямоугольник dh перпендикуляр к ac сторона ab в 2...
1 - передвижения многоклеточного организма....
1 - Дорешать. система неравенств: x=5-3y x^2+xy=5+y^2...
3 - Выразите в кубических сантиметрах 22 дм в кубе...
3 - Пересказ тарас бульба 6-7 глава ( по отдельности) (только не слишком...
3 - Спит пруд под ледяной коркой.найдите главные члены предложения...
1 - Кто такая доевнегреческая богиня гера?...
2 - Написать комплекс на исправление плоскостопия и формирования правильной...
2
Согласно этому закону, магнитное поле B на расстоянии r от проводника с током I можно выразить следующей формулой:
B = (μ₀/4π) * (I * dl × r) / r³,
где dl - элемент длины проводника, r - векторное расстояние от элемента длины до точки, в которой мы измеряем поле, μ₀ - магнитная постоянная.
Теперь мы можем рассмотреть первый проводник 1. Пусть для проводника 1 магнитное поле в точке P, где находится второй проводник 2, имеет модуль B1, а сила Ампера, действующая на проводник 1, - F1.
Таким образом, модуль силы Ампера, действующей на проводник 1, можно найти следующим образом:
F1 = I * l × B1.
Теперь рассмотрим второй проводник 2. Пусть магнитное поле в точке P, где находится проводник 2, имеет модуль B2, а сила Ампера, действующая на проводник 2, - F2.
Модуль силы Ампера, действующей на проводник 2, можно найти таким же образом:
F2 = I * l × B2.
Таким образом, отношение F1/F2 будет:
F1/F2 = (I * l × B1) / (I * l × B2) = B1/B2.
Мы предположили, что оба проводника имеют одинаковую длину, поэтому l сокращается в выражении, и мы остаемся только с отношением магнитных полей B1/B2.
Поскольку в задаче сказано, что проводники находятся в однородном магнитном поле в плоскости, перпендикулярной линиям индукции, мы можем предположить, что магнитное поле одинаково для обоих проводников, потому что их расположение относительно линий индукции одинаково.
На основании этого предположения получается, что B1 = B2, и следовательно, F1/F2 = 1.
Таким образом, разделяющая проводники сила Ампера будет одинакова для обоих проводников, и F1/F2 = 1.