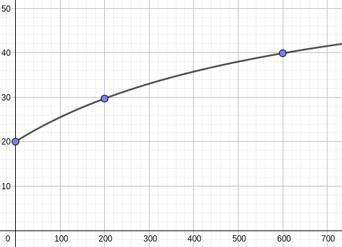
В калориметр, в котором находилось m0 = 100 г воды при температуре t = 20℃, по каплям с постоянной скоростью начинают наливать горячую воду постоянной температуры. График зависимости температуры t (в градусах Цельсия) воды в калориметре от времени t (в секундах) построили в программе GeoGebra (см. рисунок). Найдите температуру горячей воды (в градусах Цельсия), считая, что между падением капель в калориметре каждый раз успевает установиться тепловое равновесие. Потерями тепла пренебречь.

Объяснение:

m0*t0+m*t=(m0+m)*t1

m0*t0+k*m*t=(m0+k*m)*t2

к=3

t0=20

t1=30

t2=40

m*(t-t1)=m0(t1-t0)

k*m*(t-t2)=m0*(t2-t0)

m=m0(t1-t0)/(t-t1)

k*m=m0*(t2-t0)/(t-t2)

k*m=k*m0(t1-t0)/(t-t1)=m0*(t2-t0)/(t-t2)

k*m0(t1-t0)/(t-t1)=m0*(t2-t0)/(t-t2)

k*(t-t2)*(t1-t0)=(t2-t0)*(t-t1)

k*t*(t1-t0)-k*t2*(t1-t0)=(t2-t0)*t-(t2-t0)*t1

k*t*(t1-t0)-(t2-t0)*t=k*t2*(t1-t0)-(t2-t0)*t1

t*(k*(t1-t0)-(t2-t0))=k*t2*(t1-t0)-(t2-t0)*t1

t=(k*t2*(t1-t0)-(t2-t0)*t1) /(k*(t1-t0)-(t2-t0))

t=(3*40*(30-20)-(40-20)*30) /(3*(30-20)-(40-20))=60 - это ответ