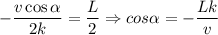В центре реки шириной L находится буй. Под каким углом к берегу лодочник должен направить лодку, чтобы причалить к бую. Скорость лодки относительно воды υ, скорость течения изменяется по мере удаления от берега по закону u=k*x, где x – расстояние до берега, k –постоянная.
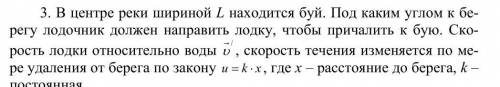
Другие вопросы по теме Физика
Популярные вопросы
- Какое попереченой сечение должен иметь стальной стержен чтобы под нагрузкой...
2 - Дана точка К, яка не лежить у площині бета, кс перпендикулярно до бета...
3 - Периметр треугольника ABC = 38 дм, точки M, N, K - середину сторон...
2 - 1)Найти диагональ осевого сечения,площадь боковой поверхности и площадь...
3 - ПРАКТИЧНЕ ЗАНЯТТЯ (Історія України 8 клас) Тема: Богдан Хмельницький...
1 - В треугольнике АВС ∠ А = 48˚, ∠ В = 94˚. Найдите последний угол блогадарю...
1 - Написать сочинение- рассуждение на тему*Водица- царица*...
2 - Самостоятельная работа 5 класс истории стр 98(Заполните таблицу) ГЕРОИ...
3 - Изобразить на координатной плоскости множество решений неравенства...
1 - Какую часть часа составляют 1 минута,25 минут,59 минут?...
2
Объяснение:
Выберем систему координат направив по вертикали ось x по горизонтали ось y
Запишем уравнения движения по каждой из осей
Выражая t из обоих уравнений получим
Решаем относительно x
Зависимость имеет вид параболы. Из условия необходимости причалить к бую, следует условие, что вершина параболы находится в центре реки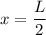
Отсюда