1. Физика
  2. В автомастерской на гладкой

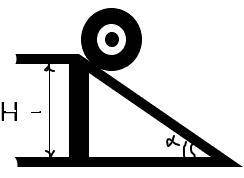
В автомастерской на гладкой горизонтальной поверхности пола находится пандус в виде сплошного клина высотой 0,5 м и углом наклона 45 градусов. Пандус прислонен к к гладкому вертикальному бетонному заграждению той же высоты. Народный "умелец" Левша скатывает с пандуса автомобильное колесо массой 15 кг без проскальзывания. . В процессе движения колеса пандус действует на заграждение с постоянной силой F=7,5 Н. какой скорости достигнет колесо у подножия пандуса, начав движение из состояния покоя. ответ представить в системе СИ, округлив до целых


В автомастерской на гладкой горизонтальной поверхности пола находится пандус в виде сплошного клина

Ann4121 Ann4121    2   14.08.2020 14:18    3

Ответы
85kurganova85 85kurganova85  15.10.2020 15:56

1 м/с

Объяснение:

Изобразим все силы действующие как на колесо так и на клин, запишем условие равновесия клина:

\displaystyle \vec{F}+\vec{N'}+\vec{P}+\vec{F_{TP}}+M\vec{g}=0

Нам надо найти величину силы трения, для этого достаточно спроецировать векторное условие равновесия на ось Х:

\displaystyle F+\frac{F_{TP}}{\sqrt{2} }-\frac{P}{\sqrt{2} }=0 = F_{TP}=P-\sqrt{2}F

Вес колеса:

\displaystyle P=N=\frac{mg}{\sqrt{2} }=\frac{15*10}{\sqrt{2} }=106 Н

Тогда, сила трения:

\displaystyle F_{TP}=106-\sqrt{2}*7.5=95 Н

Эта сила создает вращающий момент (R-радиус колеса):

\displaystyle M=F_{TP}R=95R Н*м

Скатываясь с наклонной плоскости, колесо повернется на угол (длина наклонной плоскости 0,71 м):

\displaystyle \phi=2\pi \frac{0.71}{2\pi R}=\frac{0.71}{R} рад

Сила трения совершит работу:

\displaystyle A=M\phi=95R*\frac{0.71}{R}=67.5 Дж

Конечная кинетическая энергия колеса:

\displaystyle E_k=E_p-A=mgh-A=15*10*0.5-67.5=7.5 Дж

Скорость колеса:

\displaystyle v=\sqrt{\frac{2E_k}{m}} =\sqrt{\frac{2*7.5}{15} }=1 м/с.


В автомастерской на гладкой горизонтальной поверхности пола находится пандус в виде сплошного клина
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
кира674 кира674  21.08.2019 19:50
Мальчик массой 45 кг стоит на лыжал, длина каждой лыжи 1,5 м, ширина 10см, какое давление оказывает мальчик на снег?...
Aruzhankaaaaa1 Aruzhankaaaaa1  21.08.2019 19:50
Как изменится период колебаний металлического маятника при увеличении амплитуды его колебаний в 2 раза? а. увеличится в 2 раза б. уменьшится в 2 раза в. не изменится...
DashaYazikova9 DashaYazikova9  21.08.2019 19:50
Какой потенциальной энергией обладает бетонный блок массой 1,2 тонны, поднятый на высоту 5 метров?...
Ofsi Ofsi  21.08.2019 19:50
Какой кинетическая энергией обладает теннисный мяч массой m=60г.летящая со скоростью v=180км/ч...
Енотик83 Енотик83  07.04.2020 07:46
Используя данные таблицы 34 определить неизвестные величины (единицы измерения величин записать в системе СИ), запишите уравнения силы тока I(t), напряжения U(t), заряда...
HsbHbaj HsbHbaj  07.04.2020 07:46
физика 7 класс, нужно все во...
petroura2 petroura2  06.04.2020 14:30
Резисторы R1=5(Ом) и R2=25(Ом) соединены последовательно. За какое время во втором резисторе выделится столько же теплоты, сколько в первом за 1 мин? 2. К резистору R1=5...
romamil romamil  06.04.2020 14:30
Платформа в виде сплошного диска радиусом R = 2 (м) и массой M = 100 (кг) вращается по инерции вокруг оси, совпадающей с ее осью симметрии с частотой n = 10 (мин^(– 1))....
віка812 віка812  06.04.2020 14:30
Рассмотри схеиму. Выполни необходимые вычисления и заполни таблицу​...
Hapec Hapec  06.04.2020 14:32
1) Сколько нуклонов в атоме ядра бериллия ₄⁹ Be? Сколько в нем протонов? Сколько нейтронов объясните, как вы это нашли) Я вообще не поняла...

Популярные вопросы