Уединенный шарик, облученный светом длиной волны λ = 4 нм, зарядился до потенциала φ = 0,31 кв. найдите работу выхода авых электронов с поверхности металла.

Ответы

Nastua204042 12.06.2020 04:10

По уравнению Эйнштейна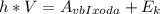 $h*V=A_{vbIxoda}+E_k$ , где V - частота излучения (Гц), h - постоянная планка (h = 6,62*10⁻³⁴ Дж*с), 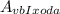$A_{vbIxoda}$ - работа выхода (Дж), 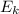E_k - максимальная энергия излучения (Дж). Запишем формулу фотоэффета (из закона сохранения энергии 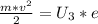$\frac{m*v^2}{2}=U_3*e$ , где U₃ - запирающие напряжение (В) - напряжение при котором ток полностью прекращается, m - масса частицы (кг), - скорость частицы (м/с), е - заряд электрона (Кл). 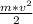В данной формуле выражение $\frac{m*v^2}{2}$ - есть кинетическая энергия 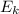E_k т.е. 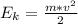$E_k=\frac{m*v^2}{2}$ . Чтогда в уравнении Энштейна кинетическую энергию можно заменить как 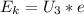E_k=U_3*e ⇒ тогда 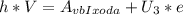$h*V=A_{vbIxoda}+U_3*e$ . Частоту можно расписать как 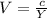$V=\frac{c}{Y}$ - где с - скорость света (с = 3*10⁸ м/с), Y - длина волны (м). Тогда ⇒ 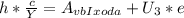$h*\frac{c}{Y}=A_{vbIxoda}+U_3*e$ отсюда выражаем находимую работу выхода: 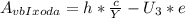$A_{vbIxoda}=h*\frac{c}{Y}-U_3*e$ . В системе СИ: 4 нм = 4*10⁻⁹ м: 0,31 кВт = 3100 В. Потенциал поля есть действующие напряжение т.е. φ = U₃; заряж электрона е = 1,6*10⁻¹⁹ Кл. Подставляем численные данные и вычисляем: