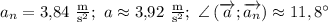Точка движется по окружности радиусом 150 см с тангенциальным ускорением 0.8 м/с2. чему равны нормальное и полное ускорение точки в конце третьей секунды после начала движения? чему равен угол между векторами полного и нормального ускорений в этот момент? (3.84 м/c2, 3.92м/c2, 11.6)
Другие вопросы по теме Физика
Популярные вопросы
- Анализ и интерпретация текста Задание. Прочитайте οтрывок из произведения...
2 - Жазғытұрым ел жайлауға көшеді.ол тасты әрең-әрең көтеріп тұр.жоғарыда ақша...
1 - - Определите жанр теста. Аргументируйте свой ответ. - Определите композиционные...
3 - Все на фотоамапивииаптвмцп ...
1 - Когда мне было шесть лет, я не знал, В каждой эпохе существуют своичто земля...
3 - 1. Укажите органическое соединение: 1) СО 2) Р2О5 3) С3Н8 4) Н3ВО3...
1 - Прочитайте отрывок из произведения В.В.Набокова «Рождество». Выпишите изобразительно...
1 - последние Определите к какой части речи относятся слова и заполните пропуски.День,...
1 - Составьте общее уравнение прямой проходящей через точки A(2;2) и B(8;4)...
2 - Розв яжіть рівняння x⁴+7x²-18=0...
1
Дано:
Найти:
1) Через три секунды скорости точки будет равна . Спроецировав на ось, проходящую по вектору скорости и, соответственно, тангенциального ускорения, получим
. Спроецировав на ось, проходящую по вектору скорости и, соответственно, тангенциального ускорения, получим 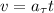
2)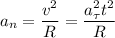
3) Т.к.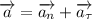 и
и 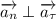 , то
, то 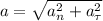
4) Пусть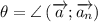 . Из наблюдений в пункте (3) имеем
. Из наблюдений в пункте (3) имеем 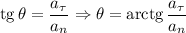
5) Произведем численный расчет
ответ.