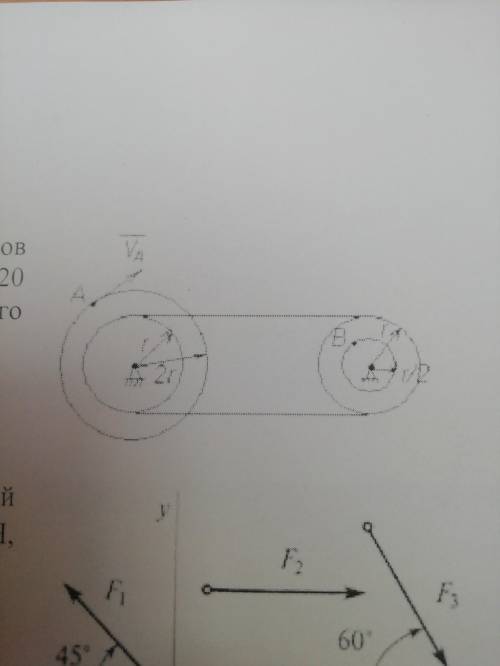
точка а одного из шкивов ременной передачи имеет скорость va20 (см/с) тогда скорость точки в другого шкива равна... (см/с)

Чтобы решить эту задачу, нужно воспользоваться законом сохранения угловых скоростей для ременной передачи. Изображение, приведенное в вопросе, демонстрирует два шкива, связанных ремнем. Пусть точка A на одном из шкивов имеет скорость va = 20 (см/с). Нам нужно найти скорость точки B на другом шкиве.

Закон сохранения угловых скоростей утверждает, что вращение ременной передачи сохраняет отношение угловых скоростей между шкивами. Другими словами, отношение угловых скоростей для двух точек на ремне будет одинаково.

Шаг 1: Определите отношение радиусов шкивов
В задаче не предоставлена информация о размерах шкивов, поэтому нам нужно предположить, что радиусы шкивов различны и обозначить их как r1 и r2.

Изображение показывает, что точка A находится на шкиве с радиусом r1, а мы ищем скорость точки B на шкиве с радиусом r2. Поэтому отношение радиусов будет r1/r2.

Шаг 2: Составьте уравнение отношения угловых скоростей
Отношение угловых скоростей между точкой A (на шкиве с радиусом r1) и точкой B (на шкиве с радиусом r2) можно записать следующим образом:

va / r1 = vb / r2

где va - скорость точки A, r1 - радиус шкива с точкой A, vb - скорость точки B, r2 - радиус шкива с точкой B.

Шаг 3: Решите уравнение для vb
Для того чтобы найти скорость точки B (vb), нам нужно решить уравнение относительно vb. Для этого сначала умножим обе части уравнения на r2:

va * r2 = vb * r1

Затем разделим обе части на r1:

vb = (va * r2) / r1

Шаг 4: Подставьте значения и рассчитайте скорость vb
Теперь мы можем подставить известные значения в уравнение и рассчитать скорость vb. Конкретные значения r1 и r2 не даны, поэтому мы не можем рассчитать точное значение vb. Однако, если бы были известны радиусы шкивов, мы могли бы использовать эти значения вместо r1 и r2.

Например, если предположить, что r1 = 5 см и r2 = 10 см, то мы можем рассчитать скорость vb следующим образом:

vb = (20 * 10) / 5

vb = 40 (см/с)

Таким образом, если предположить, что радиус первого шкива равен 5 см, а радиус второго шкива равен 10 см, то скорость точки B на втором шкиве будет равна 40 см/с.

Важно отметить, что без точных значений радиусов шкивов мы можем только предположить отношение между скоростью точки A и скоростью точки B. Если у нас есть дополнительная информация, мы можем использовать ее для получения более точного ответа.