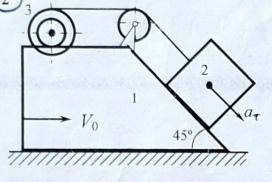
Теоретическая механика. Термех. Призма массой m1= 10 кг движется с
начальной скоростью Vo=5 м/с по гладкой
горизонтальной поверхности. В некоторый момент времени груз 2 массой m2=6кг начинает двигаться с постоянным относительным ускорением a=2 м/с^2. Определить скорость призмы через 4 с
после начала движения груза, если mз=4 кг, R3/r3=3

Добрый день! Для решения данной задачи, нам понадобятся знания из теоретической механики и законов Ньютона.

Давайте разберемся пошагово:

1. В начальный момент времени призма массой m1 движется с начальной скоростью Vo по гладкой горизонтальной поверхности. Это значит, что на призму не действуют горизонтальные силы трения.

2. В некоторый момент времени груз 2 массой m2 начинает двигаться с постоянным относительным ускорением a. Это значит, что на груз 2 действует горизонтальная сила F2, создающая ускорение.

3. Рассмотрим свободное тело груза 2. На него действуют сила тяжести Fт2 = m2*g и горизонтальная сила F2. Сумма этих сил равна массе груза 2, умноженной на ускорение a:

m2*a = F2 - m2*g

4. Рассмотрим свободное тело призмы. На нее действует сила тяжести Fтз = mз*g и горизонтальная сила Fз, создаваемая грузом 2. Сумма этих сил равна массе призмы, умноженной на ее ускорение a1:

mз*a1 = Fз - mз*g

5. Заметим, что горизонтальная сила F2, создаваемая грузом 2, равна по модулю горизонтальной силе Fз, создаваемой призмой. Таким образом, F2 = Fз.

6. Используем условие равновесия груза 2 и призмы в их совместной системе:

m2*a = F2 - m2*g
mз*a1 = F2 - mз*g

7. Подставим второе уравнение в первое:

m2*a = mз*a1

8. Заметим, что mз = 4 кг, m2 = 6 кг и a = 2 м/с². Подставим эти значения в уравнение:

6*2 = 4*a1

12 = 4*a1

9. Решим уравнение относительно a1:

a1 = 12/4

a1 = 3 м/с²

10. Ускорение a1 призмы равно 3 м/с². Найдем ее скорость через 4 секунды после начала движения груза 2.

11. Для этого воспользуемся уравнением скорости равномерно ускоренного движения:

v = vo + a*t

где v - конечная скорость, vo - начальная скорость, a - ускорение, t - время.

12. Распишем данное уравнение для призмы:

v1 = vo + a1*t

где v1 - конечная скорость призмы, vo = 5 м/с - начальная скорость призмы, a1 = 3 м/с² - ускорение призмы, t = 4 с - время.

13. Подставим значения в уравнение и решим:

v1 = 5 + 3 * 4

v1 = 5 + 12

v1 = 17 м/с

Ответ: Скорость призмы через 4 секунды после начала движения груза 2 составляет 17 м/с.