Тело свободно падает без начальной скорости с высоты h = 80 метров. Найти среднююскорость тела на последней трети дистанции. В расчетах принять g = 10 м/с2. Решите подробно Мне важно именно решение.

Средняя скорость тела - это среднее арифметическое между начальной и конечной скоростью тела на этом промежутке. Найдем их:

а) начальная скорость тела при вхождении в треть дистанции. То есть, до входа в последнюю треть, тело ещё пролетело две трети дистанции и набрало скорость v. Выведем её из общей формулы:

Учитывая, что a = g, v₀ = 0 (тело падает без начальной скорости) и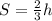 , получаем v:

б) конечная скорость тела при окончании трети дистанции. Это, собственно, конечная скорость всего пути. По той же формуле, но теперь S = h:

Средняя скорость:

vср. = (v₁ + v₂) / 2

Избавимся от цифр, приблизительно подсчитав значение цифр:

(точность очень хорошая, я округлил 1,64983 ≈ 1,65)

vср = √(1,65 * 10 м/с^2 * 80 м) ≈ 36,3 м/с