Тело массой 3 кг падает с высоты 5 м из состояния покоя и в момент падения на землю имеет скорость 8 м/с. определить силу сопротивления

Задание не вполне корректно.

Ведь сила сопротивления воздуха примерно пропорциональна квадрату скорости для тела симметричной формы.

А скорость меняется от 0 до 8 м/с.

Можно подойти к решению с упрощением на основе закона сохранения энергии.

На высоте 5 м тело имеет потенциальную энергию, равную работе по подъёму: А = mgh = 3*10*5 = 150 Дж.

На придание телу скорости в 8 м/с произведена работа А = mV^2/2 =

3*64/2 = 96 Дж.

Значит, работа на преодоление сопротивления воздуха  составила

Aтр = 150 - 96 = 54 Дж.

Вот тут и приходим к упрощению, считая силу постоянной.

Атр = F*h, отсюда F = Атр/h = 54/5 = 10,8 H.

Можно примерно определить границы изменения этой силы.

Примем F = kV² = k*(2gh) = k1h.

Тогда А = k1h*h = k1h².

То есть, работа равна площади параболы при переменной h. Площадь равна интегралу: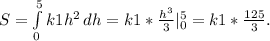

То есть, 54 = к1*(125/3)

Отсюда к1 = (54*3)/125 = 162/125 ≈ 1,3.

Сила Fтр меняется от 0 до 32,4 Н.