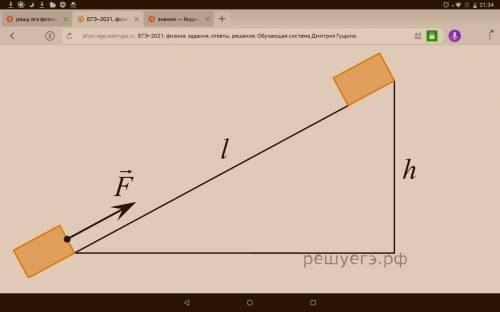
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5м, расстояние тела от поверхности Земли при этом увеличивается на h = 3м. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении совершила сила тяжести? (ответ дайте в джоулях.) Ускорение свободного падения примите равным 10м/с в степени 2 , коэффициент трения \mu = 0{,}5

Можете расписать решение?

Решение:

Для начала, нам необходимо определить ускорение тела при его движении вверх по наклонной плоскости. Для этого воспользуемся вторым законом Ньютона: F_net = ma, где F_net - сила, действующая на тело, m - масса тела, а - ускорение тела.

Сначала разложим силу F на составляющие:
1. Параллельная наклонной плоскости сила F_p = F*sin(α), где α - угол наклона плоскости.
2. Перпендикулярная наклонной плоскости сила F_n = F*cos(α).

Найдем силу трения F_t, действующую на тело по направлению вверх наклонной плоскости. Для этого воспользуемся формулой для силы трения: F_t = μ*m*g, где μ - коэффициент трения, g - ускорение свободного падения.

Поскольку сила трения направлена вниз по наклонной плоскости, а у нас трение действует вверх, то величину F_t нужно умножить на -1: F_t = -μ*m*g.

Теперь, выразим ускорение a:
F_net = F_p + F_t,
m*a = F_p + F_t,
m*a = F*sin(α) - μ*m*g,
a = (F*sin(α) - μ*m*g) / m.

Видим, что наше ускорение зависит от всех данных, которые у нас есть. Подставим значения и произведем вычисления:
m = 2 кг,
F = 30 Н,
α = угол наклона плоскости,
μ = 0,5,
g = 10 м/с^2.

У нас есть условие, что тело перемещается вверх по наклонной плоскости, то есть ускорение направлено вверх. Поэтому значению ускорения нужно дать положительную форму.

Теперь найдем ускорение a:
a = (30*sin(α) - 0,5*2*10) / 2,
a = (30*sin(α) - 10) / 2.

Далее, для определения работы силы тяжести нам необходимо знать смещение тела вдоль направления силы тяжести. В нашем случае тело перемещается вверх на расстояние h = 3 м. Таким образом, работа силы тяжести W_g определяется по формуле: W_g = m*g*h.

Подставим известные значения и произведем вычисления:
m = 2 кг,
g = 10 м/с^2,
h = 3 м.

W_g = 2*10*3 = 60 Дж.

Таким образом, сила тяжести совершит работу в размере 60 Дж.