Тело массой 1 кг равномерно вращается по окружности радиусом 1м с угловой скоростью 2рад / с найдите модуль изменения импульса тела при повороте радиус-вектора проведенного из центра круга к телу на 180 градусов
Другие вопросы по теме Физика
Популярные вопросы
- 1. Прочитать грамматическую справку по т. Словообразование - приставки...
2 - Составьте уравнение реакции и подчитайте сумму коэффициентов в уравнении:...
3 - Во и задания к документу и во для самопроверки...
3 - Рассказ М.А.Шолохова Судьба человека...
2 - Прочитайте древнегреческий миф Найдите сравнения и эпитеты после...
2 - Человек, рост которого составляет 185 см, стоит под фонарём. Его...
2 - Соцветие головка - семейство Варианты ответа: Лилейные Бобовые Крестоцветные...
2 - Укажите регион, в котором местные жители занимаются заготовкой кедрового...
3 - Являются ли словочетание превратилось в озеро, бесплодную озеро...
2 - 0,7+2\7х1.1\20-2.1\7 \=дробь...
1
Дано:
Найти: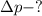
Решение. Импульс тела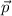 — векторная физическая величина, равная произведению массы
— векторная физическая величина, равная произведению массы 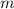 тела на скорость
тела на скорость 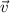 его движения:
его движения: 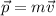
Из второго закона Ньютона:
Величину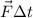 называют импульсом силы. Таким образом, импульс силы равен изменению импульса тела.
называют импульсом силы. Таким образом, импульс силы равен изменению импульса тела.
Угловая скорость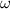 — это физическая величина, численно равная углу поворота радиуса за единицу времени:
— это физическая величина, численно равная углу поворота радиуса за единицу времени: 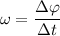 . Отсюда
. Отсюда 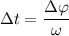
Центростремительное ускорение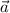 — ускорение, характеризующее быстроту изменения направления линейной скорости при движении материальной точки по окружности. Его можно определить по формуле
— ускорение, характеризующее быстроту изменения направления линейной скорости при движении материальной точки по окружности. Его можно определить по формуле 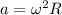
Если равнодействующая сила, приложенная к телу, перпендикулярна направлению движения тела, то тело равномерно движется по окружности и ее можно определить по второму закону Ньютона: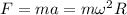
Таким образом, изменение импульса тела определим по формуле:
Определим значение искомой величины:
ответ: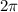 (кг· м)/с
(кг· м)/с