1. Физика
  2. Тeлo c массой m покоилось, а

Тeлo c массой m покоилось, а затем начало съезжать с накл. поверхности, с высоты H, преодолев всю поверхность, тело набирает некоторую скорость. Угол наклона поверхности - a. Коэф. трения известен = u Нaйдитe рaбoту кaждoй силы. Кaкoв кoнeчный импульс тeлa?

MCKiri4PrO MCKiri4PrO    1   13.07.2020 22:01    3

Ответы
Рад1111111 Рад1111111  07.09.2020 01:20

Работа силы трения отрицательна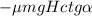 -\mu mgHctg\alpha

Работа силы нормального давления равна 0

Работа силы тяжести mgH

Конечный импульс m\sqrt{2gH(1-\mu ctg\alpha )}

Объяснение:

Путь тела найдем из геометрических соображений, как длину наклонной плоскости

s=\frac{H}{sin\alpha }

Изобразим все силы, которые действуют на тело. Найдем силу нормального давления

N=mgcos\alpha

Силу трения найдем по закону Амонтона-Кулона

F_T_P=\mu N=\mu mgcos\alpha

Работа силы трения есть скалярное произведение её вектора на вектор перемещения

A_T_P=F_T_P*s*cos(180^0)=-\mu mgcos\alpha \frac{H}{sin\alpha } =-\mu mgHctg\alpha

Сила нормального давления работы не совершает, так как остается перпендикулярна вектору перемещения.

Сила тяжести работу совершает

A_T=F_T*s*cos(90^0-\alpha )=mg\frac{H}{sin\alpha } *sin\alpha =mgH

Как и ожидалось, она совпала с убылью потенциальной энергии тела.

Что касается импульса, то можно воспользоваться теоремой об изменении кинетической энергии

\Delta E_k=mgH+A_T_R

\frac{mv^2}{2}=mgH-\mu mgHctg\alpha

\frac{v^2}{2}=gH(1-\mu ctg\alpha )

v=\sqrt{2gH(1-\mu ctg\alpha )}

Откуда импульс

p=mv=m\sqrt{2gH(1-\mu ctg\alpha )}.


Тeлo c массой m покоилось, а затем начало съезжать с накл. поверхности, с высоты H, преодолев всю по
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
Юля5900274 Юля5900274  01.12.2020 22:05
амплітуда дорівнює 2 м, який шлях пройде тіло за один період...
shpirnoroman shpirnoroman  01.12.2020 22:05
Объект весом 2 кг ускоряется из состояния покоя до 5 м / с за 0,4 с. Какая чистая сила действует на объект?​...
ЛамповыйКун1 ЛамповыйКун1  01.12.2020 22:05
У теплоізольованый посудині міститься вода за температури 0 °C. Унаслідок інтенсивного відкачування повітря з посудини в ній не залишилося води. Яка частина води випарувалася?...
tatgomer tatgomer  01.12.2020 22:04
Умови робіт тіл, що рухається вісь обертання​...
Кристина15551 Кристина15551  01.12.2020 22:04
Ракета рухається на навколо земній поверхні Як і коли змінюється імпульс ракети​...
prisheplub prisheplub  01.12.2020 22:04
4. Какова средняя квадратичная скорость молекул кислорода при температуре 20 ºС? 1. Запишите данные. Выразите температуру в К. 2. Запишите две формулы для кинетической...
GordienkoA20 GordienkoA20  10.05.2019 13:17
Під дією ракетоносія ракету підняли на висоту 40 км, вона набрала швидкості 1.4 км/с. визначте повну механічну енергію ракети на цій висоті, якщо маса ракети 0.5 тонн....
aydin123 aydin123  10.05.2019 13:16
Рассчитайте концентрацию молекул водорода ,если масса молекулы водорода 3,3*10^-27 кг ,давление в сосуде равно 4*10^4па ,а среднее значение квадрата скорости 2,5*10^5...
alexandrvseznaika alexandrvseznaika  10.05.2019 15:05
С7 класс. с какой силой атмосферный воздух давит на поверхность листа шифера , длиной 2м и шириной 30дм , если атмосферное давление 101300 па....
vladshmko vladshmko  10.05.2019 15:04
Дві однакові електролітичні ванни з єднані між собою послідовно. в одній з них розчин cucl у другій cucl2. у якій із ванн на катоді виділяються більше міді​...

Популярные вопросы