Тело бросают вертикально вверх со скоростью 5,2 м/с. одновременно с предельной высоты, которой оно может достичь, бросают вертикально вниз другое тело с той же начальной скоростью. определить время, по истечении которого тела встретятся.
Другие вопросы по теме Физика
Популярные вопросы
- Мне найти стихотворение для олимпиады 10 класса,6-7 строк хватит)...
3 - Вправа 139(а) 1.змінюючи іменники,склади и запиши з поданих слів речення.визнач...
3 - На подвір ї гуляла однакова кількість свиней і качок. разом у них було 18...
2 - ответьте какие ! 1. атазаң деген ұғымды қалай түсінесіндер? 2. конституция...
2 - Рассчитайте, сколько граммов пентадиен-1,2 потребуется для получения 720...
2 - Составить предложение со словом заброшенно и обижено...
1 - 13. какую команду используют в графическом редакторе paint для измене- ния...
1 - Какие координаты у санкт петербурга...
1 - Уравнения: (d-389)*3=807,8*(5400-s)=5536,t:...
2 - Запишите числа в порядке убывания: 345/23, 75/11, 267/14, 952/356, 51/4...
3
координаты будут равны
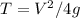
пусть y направлена вверх
мы знаем что координата в любой момент времени y(t) = y0+v0yt+gyT^2/2
y1=v0T-gT^2/2 y2=V0^2/2g - VoT + gT^2/2
y1=y2
V0t - gt^2 = V0^2/2g - V0T - gt^2/2
Здесь V0^2/2g - H (maximal)
2V0T = V0^2/2g
4gT=V0^2
V Начальня скорость, g ускорение свободного падения. надеюсь дальше сами справитесь
y(t) = y0+v0yt+gyT^2/2
y1=v0T-gT^2/2 y2=V0^2/2g - VoT + gT^2/2
y1=y2
V0t - gt^2 = V0^2/2g - V0T - gt^2/2
Здесь V0^2/2g - H (maximal)
2V0T = V0^2/2g
4gT=V0^2
найдем У = 5.2^2 / 2*10 = 1.352
ТЕПЕРЬ ищем Т = V0^2 / 4g = 5.2^2 / 40 = 0.676 и теперь все подставляем в первую формулу V0t - gt^2 = V0^2/2g - V0T - gt^2/2 = -4.3