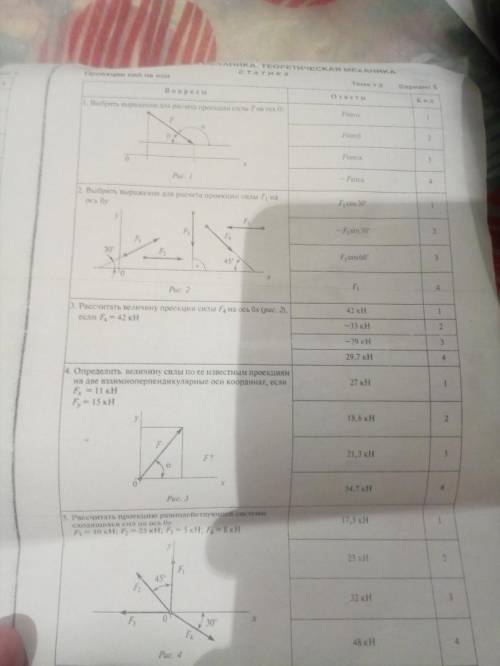
Техническая механика.Теоретичская механика Статика Проекция сил на оси тема 1,2 Вариант 5 Нужно с решениями,а не овтеты с сборника

Изображенная на картинке конструкция состоит из трех стержней, которые соединены в одной точке. На эти стержни действуют силы F1 = 50 Н, F2 = 70 Н и F3 = 120 Н, направленные под определенным углом.

Чтобы решить эту задачу, нам необходимо разложить каждую из сил на две составляющие: горизонтальную и вертикальную. Затем мы сложим все вертикальные и горизонтальные составляющие каждой силы отдельно, чтобы получить полную вертикальную и горизонтальную составляющие.

Начнем с разложения силы F1. Мы знаем, что угол α между F1 и осью X равен 60 градусов. Чтобы найти горизонтальную составляющую этой силы (F1х), мы используем формулу Fх = F * cos(α), где F - величина силы, α - угол между силой и осью X. Подставляя известные значения, получаем F1х = 50 * cos(60) = 50 * 0,5 = 25 Н.

Теперь найдем вертикальную составляющую этой силы (F1у). Мы используем формулу Fу = F * sin(α), где F - величина силы, α - угол между силой и осью X. Подставляя известные значения, получаем F1у = 50 * sin(60) = 50 * 0,866 ≈ 43,3 Н.

Аналогичным образом разложим силы F2 и F3. Для силы F2, угол β равен 45 градусов. Она будет иметь горизонтальную составляющую (F2х) равную F2х = 70 * cos(45) ≈ 49,5 Н и вертикальную составляющую (F2у) равную F2у = 70 * sin(45) ≈ 49,5 Н.

Для силы F3, угол γ равен 30 градусов. Она будет иметь горизонтальную составляющую (F3х) равную F3х = 120 * cos(30) ≈ 103,9 Н и вертикальную составляющую (F3у) равную F3у = 120 * sin(30) = 120 * 0,5 = 60 Н.

Теперь сложим все вертикальные составляющие и горизонтальные составляющие, чтобы получить полную вертикальную и горизонтальную составляющие.

ΣFх = F1х + F2х + F3х = 25 Н + 49,5 Н + 103,9 Н ≈ 178,4 Н
ΣFу = F1у + F2у + F3у = 43,3 Н + 49,5 Н + 60 Н = 152,8 Н

Таким образом, полная вертикальная составляющая равна 152,8 Н, а полная горизонтальная составляющая равна 178,4 Н.

Ответ: полная вертикальная составляющая равна 152,8 Н, полная горизонтальная составляющая равна 178,4 Н.