1. Физика
  2. Свысотой 9,62 м бросили

Свысотой 9,62 м бросили мячик вертикально вверх с начальной скоростью 5м/с. определите время полетаи скорость тела в момент удара о землю

enbasmanovan enbasmanovan    3   28.09.2019 16:01    6

Ответы
CorrupteD CorrupteD  09.10.2020 00:53
По условию:

h₀ = 9,62 м;

V₀ = 5 м/с.

t, V - ?

Решение:

В данной задаче следует рассматривать три момента:

1) Момент броска мяча, V₀ = 5 м/с, h₀ = 9,62 м.

2) Момент, когда мяч достигает верхней точки, V' = 0 м/c,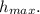 h_{max}.

3) Момент приземления, h = 0 м, t - ?

Время полёта поделим на 2 части: время от момента (1) до момента (2) (пусть t₁) и далее от момента (2) до (3) (пусть t₂). Значит, t = t₁ + t₂.

Время t₁ определим из уравнения зависимости скорости от времени:

V' = V_0 - gt_1,

t_1 = \frac{V_0 - V'}{g} = \frac{5-0}{10} = 0,5 (c).

Перед нахождением времени t₂ нужно найти максимальную высоту, на которой мячик остановится, перед тем как начать падать. Для этого воспользуемся уравнением движения:

h_{max} = h_0 + V_0t_1 - \frac{gt_1^2}{2} = 9,62 + 5*0,5 - \frac{10*0,5^2}{2} = 10,87 (м).

С текущими данными мы сможем найти скорость перед приземлением, используя следующую формулу и учитывая, что V' = 0:

h_{max} = \frac{V^2 - V'^2}{2g} = \frac{V^2}{2g},

V = \sqrt{2gh_{max}} = \sqrt{2*10*10,87} = 14,74 (м/с).

Теперь, зная максимальную высоту, найдём время t₂ через уравнение движения:

h = h_{max} - \frac{gt_2^2}{2} = 0,

t = \sqrt{\frac{2h_{max}}{g}} = \sqrt{\frac{2*10,87}{10}} = 1,47 (c).

Таким образом, t = 0,5 + 1,47 = 1,97 (c).

ответ: 1,97 с; 14,74 м/с.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
REDUCE007 REDUCE007  14.07.2019 18:00
1. почему магнитная стрелка компаса перестаёт показывать на север, если неподалёку от компаса находится провод с эл током? 2. при какой силе тока через проводник проходит...
NezNeika NezNeika  14.07.2019 18:00
Квертикальной стене прижали деревянный брусок массой 1,5кг. коэффициент трения бруска о стену составляет 0,3. с какой наименьшей силой необходимо прижимать брусок к стене,...
rezistol228 rezistol228  14.07.2019 18:00
Во сколько раз надо изменить длину маятника, чтобы период колебания изменился в 2 раза?...
msyesta msyesta  09.07.2019 06:50
Сосуд, содержащий 10л воздуха при давлении 1мпа, соединяют с пустым сосудом вместимостью 4л. определите давление, установившееся в сосудах при изотермическом процессе....
Nerzul2828818 Nerzul2828818  03.03.2021 17:06
Неподвижный блок не даёт выигрыша в силе Подвижный блок даёт выигрыш в силе в 2 раза Система блоков, Выирыш в силе в 3 дающая раза Система блоков, дающая выигрыш в силе в...
KristheMalen KristheMalen  03.03.2021 17:05
4al Определите площадь опоры прибора, если его масса800 кг, а производимое им давление 200 кПа.​...
lambert1337 lambert1337  03.03.2021 17:05
Выполнить ОБА варианта Пишите номер варианта Буква вопроса, номер ответа и переписывание содержание ответа Если это задача, то ответ принимается только при наличии решения...
Маширо11 Маширо11  03.03.2021 17:04
Во время изобарного нагревания 0,32 кг метана CH4 его температура изменилась на 10⁰С. Какое количество теплоты получил газ? Универсальная газовая постоянная R=8,3 Дж/(моль·К)....
vaxaxa1717 vaxaxa1717  03.03.2021 17:04
Бадью с раствором поднимают при неподвильного блока на высоту 10м,действуя с силой 300Н. Найти к.п.д. установки,если масса бадьи 25 кг...
ksyushenkа ksyushenkа  08.02.2021 21:17
рівень води у u-подібній трубці на 15 см нижчий за краї трубки. трубку ліворуч повністю заповнюють гасом визнач висоту стовпа гасу...

Популярные вопросы