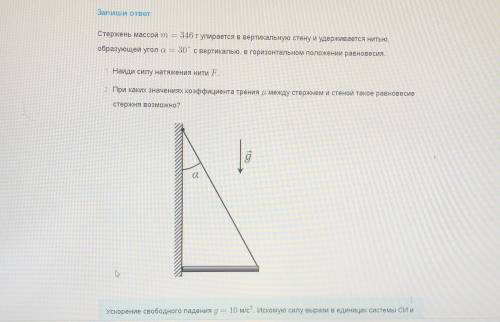
Стержень массой m=346 г упирается в вертикальную стену и удерживается нитью . Образующей угол альфа 30 градусов с вертикалью

жиз сам не могу решить но 10 балов нужни

Давайте разберем этот вопрос пошагово.

Итак, у нас есть стержень, который упирается в вертикальную стену и удерживается нитью. Масса стержня составляет 346 грамм. Нить, держащая стержень, образует угол α в 30 градусов с вертикалью.

Первым шагом, который мы можем сделать, это найти горизонтальную силу, действующую на стержень. Эта сила вызвана натяжением нити и направлена вдоль поверхности стены.

Для этого мы можем использовать разложение силы натяжения на горизонтальную и вертикальную составляющие. Горизонтальная составляющая силы натяжения равна T * cos(α), где T - сила натяжения нити.

Вторым шагом, мы можем найти силу натяжения нити по вертикали. Для этого мы можем использовать разложение силы тяжести стержня на горизонтальную и вертикальную составляющие. Вертикальная составляющая силы тяжести равна m * g, где g - ускорение свободного падения.

Третий шаг состоит в том, чтобы установить, что сумма вертикальных сил должна быть равна нулю, так как стержень находится в равновесии по вертикали. Следовательно, сила натяжения нити по вертикали должна быть равна вертикальной составляющей силы тяжести стержня.

Четвертым шагом, мы можем решить уравнение, чтобы найти силу натяжения нити. Таким образом:

T * sin(α) = m * g.

Известными данными являются масса стержня m = 346 г и угол α = 30 градусов. Значение ускорения свободного падения g примерно равно 9.8 м/с^2.

Подставив известные значения, мы можем решить уравнение:

T * sin(30) = 0.346 * 9.8,
T * 0.5 = 3.3908,
T = 6.7816.

Таким образом, сила натяжения нити T равна примерно 6.7816 Н (ньютон).

Это решение позволяет определить силу, с которой нить держит стержень, когда он упирается в вертикальную стену. Используя эту информацию, можно дальше анализировать ситуацию и решать другие задачи, связанные с этим экспериментом или силами, действующими на стержень и нить.