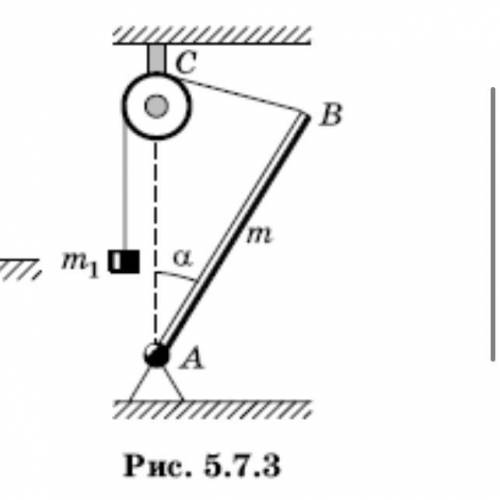
Стержень АВ массой m = 10 кг прикреплен к неподвижной опоре шарниром А и может вращаться в вертикальной плоскости. К концу В стержня прикреплена нить. Нить перекинута через блок С и к ней подвешен груз массой m1 = 2,5 кг. Оси блока С и шарнира А расположены на одной вертикали, причем АС = АВ. Найти, при каком угле а между стержнем и вертикалью система будет в равновесии. Какая сила FАВ действует вдоль стержня в точке А? Является ли равновесие устойчивым?
Другие вопросы по теме Физика
Популярные вопросы
- 52 956 : 3= 52 960 : 32=52 800 : 320=142 765 :5=142 750 : 50=142 750 : 125=892...
1 - Гелий массой 25г изобарно нагрели на 400 К. Удельная теплоёмкость гелия с=5290...
3 - Назовите причины появления скотоводство и земледелия ...
2 - Электротехника. цепь с сопротивлением, индуктивностью, ёмкостью решить задачу,...
1 - 674 выполните действие можете сделать по действиям...
2 - СОР ПО ВСЕМИРНОЙ ИСТОРИИ 6 КЛАСС 2 ЧЕТВЕРТЬ ТАМ НАПИСАНО СОЧ ЭТО ПО ОШИБКЕ дайю...
1 - В двух стаканах налит раствор вещества Х. 2б В один стакан добавили три капли индикатора...
1 - прочитайте текст и ответьте на вопросыв Казахстане с 1921 по 1954 год да по политическим...
2 - Боже дайте ответ до вечера 1. Какой возраст Земли? 2. Какая она была первоначальная?...
1 - Сейтқұл ел қамы үшін қандай әрекетке барды? ...
1
1. Вес стержня АВ, который направлен вниз и его модуль равен Fг = m * g, где m - масса стержня, а g - ускорение свободного падения.
2. Вес груза, который также направлен вниз и его модуль равен Fгруза = m1 * g, где m1 - масса груза.
Таким образом, сумма модулей внешних сил, действующих на систему, равна Fг + Fгруза.
Далее, рассмотрим силы внутри системы.
3. Натяжение нити натягивает блок С и действует вдоль нити.
Поскольку система находится в равновесии, сумма моментов сил относительно точки А равна нулю. Момент силы Fг относительно A равен Fг * AB * sin(a), где AB - длина стержня.
Таким образом, уравнение равновесия будет иметь вид:
Fг * AB * sin(a) - Fгруза * AB * sin(a) = 0.
Решим его относительно sin(a):
Fг * AB * sin(a) = Fгруза * AB * sin(a),
Fг = Fгруза.
Подставляем значения:
m * g = m1 * g,
10 * 9.8 = 2.5 * 9.8.
Решая уравнение, получим:
98 = 24.5.
Так как 98 не равно 24.5, то равновесие данной системы невозможно.
Поэтому сила FАВ, действующая вдоль стержня в точке А, также не может быть определена.
Ответ: равновесие данной системы невозможно.