Средняя квадратичная скорость молекул кислорода при 927 градусов равна 960м\с. какова средняя квадратичная скорость этих молекул при температуре газа 27 градусов?
Другие вопросы по теме Физика
Популярные вопросы
- Что нового появляется у инфузории в отличие от амёбы...
1 - Найдите расстояние между точками a(−6,5) и b(1 1/2) на координатной прямой. выберите...
2 - Жуль верн подорож на мисяць що порадив герой роману щоб вода не виповзала назвині...
1 - Доведіть: якщо пряма перетинає одну з двох паралельних площин, то вона перетинає...
3 - Проверочные слова к слову кровати диваны корзине скамье коробки катушки бумажке...
3 - Как соотносятся понятия долг и совесть?...
3 - Решите уровнение 8х+1=7х-2; 5х-3+3х-2. 0,75х+1,25х-1; 0,01х-2+0,01х-3 3х+2=2х+5+х...
3 - Минусовая и плюсовая маркировка. определите , какая маркировка у этих слов : на...
2 - Ученикам 7 класса вопрос где расположена наиболее сухая и жаркая область африки?...
2 - Основной сплав металлов давший название эпохе...
2
ответ: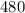 м/с
м/с
Объяснение:
Средняя квадратичная скорость молекул кислорода при 927 °C равна 960м\с. Какова средняя квадратичная скорость этих молекул при температуре газа 27 °C? - полное условие задачи
Конечно же на данный вопрос можно ответить и не зная что "Средняя квадратичная скорость молекул кислорода при 927 °C равна 960м\с." Но если данную задачу нужно решить обязательно принимая в расчет численные данные данные указанные выше тогда решение будет выглядеть следующим образом.
Дано:
------------------------------------------------------
Согласно основному уравнению МКТ
Также мы знаем что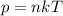
Отсюда
При