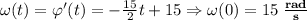Спо . не могу разобраться, олимпиадные)
Другие вопросы по теме Физика
Популярные вопросы
- Становище національних меншин і міжнаціональних відносин в країнах центрально-східної...
2 - Гипотенуза прямоугольного треугольника равна18см, чему равна медиана проведенная...
3 - Выпишите 5 предложений с орфаграммой правописани не с существительными...
2 - Средняя линия равнобедренного треугольника равна 5 см, а его периметр...
2 - Дано вектора а(3: -5) и b(x: 6) при каком значении х вектора перпендикулярные....
2 - Принадлежит ли графику функции y=x^7 точка (2; ; -128); (-3; 2187)...
1 - Скоординатами. 15 . как можно быстрей....
1 - 50 человек выполняют работу за 6 месяцев. сколько времени эту же работу...
3 - Доказать что y=x³- 4x нечётная функция...
2 - Анализ стихотворения сороковые д. самойлова по плану: 1. создания. 2.жанр...
1
2.3 Момент инерции системы точек вычисляется по формуле: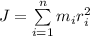 , где
, где 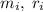 - соответственно масса i-той точки и расстояние от i-той точки до оси.
- соответственно масса i-той точки и расстояние от i-той точки до оси.
Для начального положения: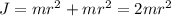 ; для конечного:
; для конечного: 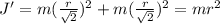 ; Получили, что момент инерции системы уменьшился в два раза.
; Получили, что момент инерции системы уменьшился в два раза.
2.2 Так как зависимость параболическая, то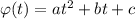 ;
;
Заметим, что коэффициент c - есть ордината точки пересечения параболы с осью OY (действительно, чтобы в этом убедиться достаточно подставить x=0).
Координаты вершины также достаточно просто вычислить. Имеем: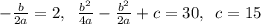 ; Отсюда легко вывести, что
; Отсюда легко вывести, что 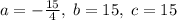 ; Итак,
; Итак, 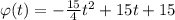 , значит,
, значит,