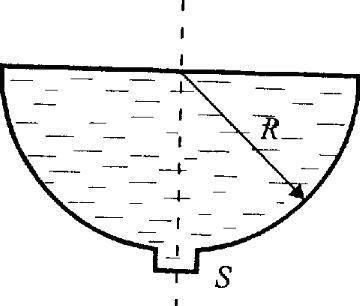
Сосуд в виде полусферы радиусом R = 10 см до краев наполнен водой. На дне сосуда имеется отверстие площадью поперечного сечения S = 4 мм^2 . Определите время, за которое через это отверстие выльется столько воды, чтобы ее уровень в сосуде понизился на 5 см с полным решением!

Для решения этой задачи, мы можем использовать закон Торричелли для вытекания жидкости через отверстие в сосуде. Закон Торричелли гласит, что скорость вытекания жидкости через отверстие пропорциональна корню из разности уровней жидкости над отверстием и свободной поверхностью жидкости.

Изначально, уровень жидкости в сосуде находится на высоте R = 10 см, а мы хотим определить время, за которое уровень жидкости понизится на 5 см.

1. Определим разность уровней жидкости над отверстием и свободной поверхностью жидкости:
h = R - 5 см = 5 см

2. Запишем закон Торричелли для нашей задачи:
v = k√h

где v - скорость вытекания жидкости, k - коэффициент, характеризующий условия вытекания жидкости (константа), а h - разность уровней жидкости.

3. Теперь найдем значение коэффициента k. Для этого необходимо воспользоваться площадью поперечного сечения отверстия S = 4 мм^2 и коэффициентом сопротивления вытеканию жидкости через отверстие C. Запишем формулу для скорости вытекания через отверстие:
v = CS

где C - коэффициент сопротивления вытеканию жидкости через отверстие, S - площадь поперечного сечения отверстия.

Так как в задаче не указаны данные для определения этого коэффициента, мы предположим, что его значение равно 1 (это предположение сделано для упрощения вычислений, в реальности необходимо знать точное значение коэффициента сопротивления).

Таким образом, у нас получается:
v = S

4. Теперь можем записать закон Торричелли с использованием найденного значения коэффициента:
v = k√h
S = k√h

Подставим значение площади поперечного сечения S:
4 мм^2 = k√5 см

Приведем единицы измерения к одному виду:
4 мм^2 = k√(5/10) см
4 мм^2 = k√(1/2) см

Возведем обе части уравнения в квадрат:
(4 мм^2)^2 = (k√(1/2) см)^2
16 мм^4 = k^2 * (1/2) см^2

Упростим уравнение, решив его относительно k^2:
k^2 = (16 мм^4) / (1/2) см^2
k^2 = 32 мм^4/см^2

Извлечем корень из обеих частей уравнения:
k = √(32 мм^4/см^2)
k = sqrt(32) мм^2/см

Таким образом, k = sqrt(32) мм^2/см.

5. Подставим значение разности уровней жидкости и найденное значение коэффициента в закон Торричелли:
v = k√h
v = sqrt(32) мм^2/см * √5 см

Упростим уравнение:
v = sqrt(32 * 5) мм = sqrt(160) мм

Таким образом, скорость вытекания жидкости равна sqrt(160) мм.

6. Теперь определим время, за которое выльется нужное количество жидкости. Для этого воспользуемся формулой:

время = объем / скорость

Объем вылитой жидкости можно определить как площадь поперечного сечения отверстия, умноженную на высоту, на которую понизится уровень жидкости:
объем = S * H

Подставим известные значения и найденное значение скорости:
время = (S * H) / скорость
время = (4 мм^2 * 5 см) / sqrt(160) мм

Упростим уравнение:
время = 20 мм * sqrt(160) мм / sqrt(160) мм

Сократим sqrt(160) мм:
время = 20 мм.

Таким образом, время, за которое выльется нужное количество жидкости, равно 20 мм.