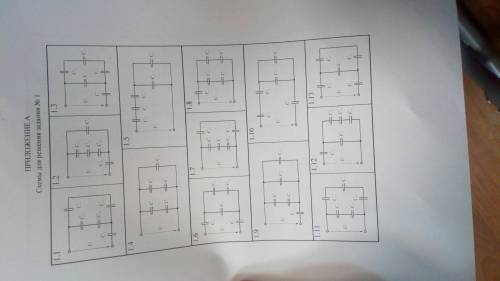
Смешанное соединение конденсаторов. Дана батарея конденсаторов соединенных смешанным и подключенных к сети переменного тока напряжением 220В. Схема включения соответствует варианту задания и изображена на схемах 1.1 -1.25 в приложении А (страницы 30-31), по заданным в таблице 1.1 параметрам рассчитать: 1) Эквивалентную (общую) емкость батареи конденсаторов 2) Заряд каждого конденсатора 3) Напряжение на каждом конденсаторе 4)Энергию каждого конденсатора У МЕНЯ ВАРИАНТ 12, рисунок 1.12

Другие вопросы по теме Физика
Популярные вопросы
- Восновании пирамиды прямоугольный треугольник с гипотенузой a, каждое боковое...
1 - 99 , определить стилистическую принадлежность слов: обставлена, обиты, разрисован,...
3 - Реши уравнение y: 2=42+58 как можно быстрей...
1 - ❤! ❤и решите в виде уравнения! ❤ в спортивном лагере 5/9 прибывших туристов...
1 - Решите пропорцию. 1) икс делим на одну челую три пятых равно три целых две...
1 - Найдите значение выражения x^2-5x-14=0...
3 - Какие вещества корень растения высасывает почвы? 1)минеральные 2)органические...
2 - На одной пластине конденсатора заряд -2мккл, на другой - +2мккл. электроемкость...
2 - Iwish for conversationsome but for obvious reasons there are not many around....
1 - План к рассказу как мы летали в космос...
1
1) Для начала, нам необходимо определить эквивалентную (общую) емкость батареи конденсаторов. В задании дан вариант 12, где смешанное соединение конденсаторов показано на рисунке 1.12. На схеме видно, что есть два параллельно соединенных конденсатора (С1 и С2), а затем они соединены последовательно с конденсатором С3.
Для определения эквивалентной емкости батареи смешанных конденсаторов, нам нужно использовать формулу для расчета общей емкости соединения конденсаторов параллельно и последовательно.
1.1) Посчитаем эквивалентную емкость конденсаторов С1 и С2, которые соединены параллельно:
В данном случае, мы просто складываем емкости: Сэкв = С1 + С2.
1.2) Теперь мы можем рассчитать эквивалентную емкость конденсаторов Сэкв и С3, которые соединены последовательно:
Для этого используем формулу:
1/Собщ = 1/Сэкв + 1/С3.
2) Теперь, когда мы определили эквивалентную емкость батареи конденсаторов, можем перейти ко второму вопросу: заряд каждого конденсатора.
Для расчета заряда каждого конденсатора мы можем использовать формулу:
Q = C * U, где Q - заряд, C - емкость, U - напряжение.
2.1) Рассчитаем заряд конденсатора С1:
Q1 = C1 * U1.
2.2) Точно так же, рассчитаем заряд конденсатора С2:
Q2 = C2 * U2.
2.3) Наконец, определим заряд конденсатора С3:
Q3 = C3 * U3.
3) Теперь, когда у нас есть заряд каждого конденсатора, можем перейти к третьему вопросу: напряжение на каждом конденсаторе.
3.1) Напряжение на конденсаторе С1 равно: U1.
3.2) Напряжение на конденсаторе С2 равно: U2.
3.3) Напряжение на конденсаторе С3 равно: U3.
4) Наконец, перейдем к последнему вопросу: энергия каждого конденсатора.
Для расчета энергии каждого конденсатора мы можем использовать формулу:
E = (1/2) * C * U^2, где E - энергия, C - емкость, U - напряжение.
4.1) Рассчитаем энергию конденсатора С1:
E1 = (1/2) * C1 * U1^2.
4.2) Точно так же, рассчитаем энергию конденсатора С2:
E2 = (1/2) * C2 * U2^2.
4.3) И, наконец, найдем энергию конденсатора С3:
E3 = (1/2) * C3 * U3^2.
Важно отметить, что для расчетов необходимо знать значения емкостей (С1, С2, С3) и напряжения (U1, U2, U3), которые в данном случае заданы в таблице 1.1. Подставив эти значения в соответствующие формулы, мы можем рассчитать ответы на каждый из вопросов задачи.
Загрузка таблицы вместе с рисунком 1.12 не предоставлена, поэтому я не могу продемонстрировать полное решение для варианта 12. Однако, с помощью вышеуказанных шагов и представленных формул, вы сможете решить эту задачу самостоятельно, используя данные из своего учебника или лекций по физике.