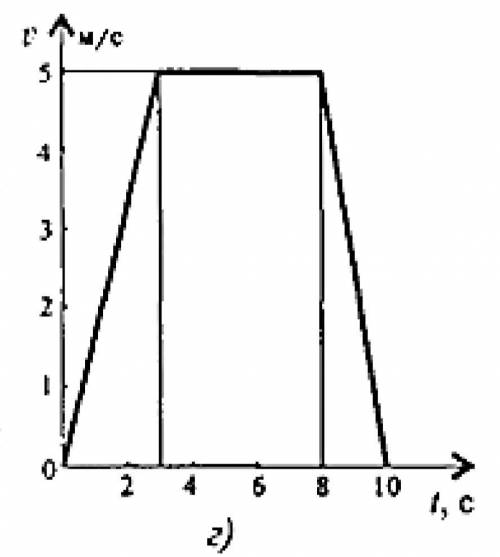
Скорость кабины лифта изменяется согласно графика. Определить величину натяжения каната, на котором подвешен лифт, при подъеме и
опускании. По максимальной величине натяжения каната определить потребную
мощность электродвигателя.
Масса, m кг = 450
КПД= 0,75

Для решения этой задачи нам потребуется использовать второй закон Ньютона (закон движения), а также формулу для определения мощности электродвигателя.

Для начала, нам необходимо определить силу, действующую на лифт при его подъеме и спуске. Для этого воспользуемся вторым законом Ньютона, который гласит: сумма всех сил, действующих на тело, равна произведению массы тела на его ускорение.

В данной задаче сила натяжения каната является основной силой, действующей на лифт, поэтому мы можем использовать ее для определения ускорения.

1. Подъем лифта:
Сначала определим ускорение лифта. По графику видно, что в начале и конце движения кабины лифта ее скорость равна 0, значит, в эти моменты ускорение также равно 0.

На участке AC, скорость лифта увеличивается, поэтому в этом случае есть ускорение. Мы можем определить его, используя разницу скоростей и разницу времени между точками A и C. Для этого воспользуемся формулой ускорения: ускорение (a) = (конечная скорость - начальная скорость) / время.

Учитывая, что начальная скорость равна 0, конечная скорость на участке AC равна 6 м/с, а время равно 3 секундам (из графика), мы можем вычислить ускорение:
a = (6 м/с - 0 м/с) / 3 с = 2 м/с^2.

Теперь мы можем определить силу натяжения каната при подъеме, используя второй закон Ньютона:
сила натяжения каната = масса * ускорение.

В данном случае масса лифта равна 450 кг, а ускорение равно 2 м/с^2, поэтому:
сила натяжения каната = 450 кг * 2 м/с^2 = 900 Н (ньютон).

2. Спуск лифта:
Аналогично определим силу натяжения каната при спуске. В этом случае ускорение будет отрицательным, так как лифт замедляется.

На участке CB, скорость лифта уменьшается, поэтому есть отрицательное ускорение. Для определения его значения воспользуемся той же формулой ускорения:
ускорение (a) = (конечная скорость - начальная скорость) / время.

Согласно графику, конечная скорость равна -6 м/с, что означает, что она направлена вниз, а начальная скорость равна 0 м/с. Время также равно 3 секундам.
Таким образом,
a = (-6 м/с - 0 м/с) / 3 с = -2 м/с^2.

Теперь мы можем определить силу натяжения каната при спуске:
сила натяжения каната = масса * ускорение.

В данном случае масса лифта равна 450 кг, а ускорение равно -2 м/с^2, поэтому:
сила натяжения каната = 450 кг * -2 м/с^2 = -900 Н (ньютон).

3. Определение мощности электродвигателя:
Мощность (P) электродвигателя, необходимая для подъема и опускания лифта, можно определить, использовав следующую формулу:
мощность = работа / время,

где работа (W) вычисляется по следующей формуле:
работа = сила * путь.

Поскольку высота изменяется, а сила натяжения каната постоянна на каждом участке движения, нам необходимо рассчитать работу для каждого участка отдельно.

На участке AC, сила натяжения каната равна 900 Н, а путь (S) равен 10 м (из графика). Тогда:
работа на участке AC = сила * путь = 900 Н * 10 м = 9000 Дж (джоулей).

На участке CB, сила натяжения каната равна -900 Н (заметьте, что она отрицательная), а путь (S) также равен 10 м. Тогда:
работа на участке CB = сила * путь = -900 Н * 10 м = -9000 Дж (джоулей).

Общая работа, необходимая для подъема и опускания лифта, равна сумме работ на каждом участке:
общая работа = работа на участке AC + работа на участке CB = 9000 Дж + (-9000 Дж) = 0 Дж.

Теперь, используя формулу для определения мощности электродвигателя, мы можем вычислить ее:
мощность = работа / время.

В данном случае работа равна 0 Дж, а время равно 6 секундам (из графика), поэтому:
мощность = 0 Дж / 6 с = 0 Вт (ватт) - электродвигатель не требует мощности для подъема и опускания лифта на данном участке.

Итак, величина натяжения каната, на котором подвешен лифт, при подъеме и опускании равна 900 Н (ньютон). Потребная мощность электродвигателя равна 0 Вт (ватт).