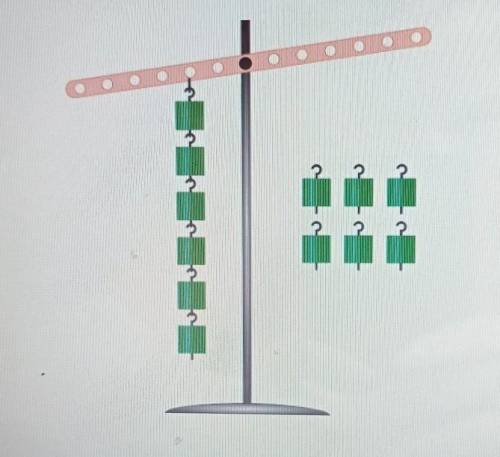
Сколько вариантов уравновешивания рычага возможно в данном случае при данном количестве дополнительных грузов (6)? Справа грузы (один, несколько или все) можно подвешивать только в
одном месте, а грузы слева перевешивать нельзя!​

Чтобы решить эту задачу, давайте сначала разберемся с условиями. У нас есть рычаг, который можно считать прямой. На этом рычаге есть шесть точек, в которых можно подвесить грузы. Справа от центра рычага могут быть один, несколько или все грузы, в то время как грузы слева от центра рычага перевешивать нельзя.

Для уравновешивания рычага мы должны распределить грузы таким образом, чтобы моменты сил справа и слева от центра рычага были равны. Момент силы определяется произведением силы на расстояние от ее точки приложения до центра вращения.

Теперь рассмотрим возможные варианты, при которых рычаг будет уравновешен.

1. Пусть у нас есть только один дополнительный груз. В этом случае мы можем повесить его в любую из шести точек на рычаге. Это дает нам 6 возможных вариантов.

2. Пусть у нас есть два дополнительных груза. Теперь мы должны выбрать, в каких точках мы будем их подвешивать. При этом мы можем подвесить первый груз в любую из шести точек, а второй груз - в оставшиеся пять точек (у нас уже будет одна точка занята). Всего это дает нам 6*5 = 30 возможных вариантов.

3. Продолжая аналогичным образом, при трех дополнительных грузах мы можем выбрать первый груз для подвешивания из шести точек, второй груз - из оставшихся пяти точек, и третий груз - из четырех оставшихся точек. Таким образом, имеем 6*5*4 = 120 возможных вариантов.

4. При четырех дополнительных грузах мы можем выбрать первый груз из 6 точек, второй груз - из 5 точек, третий груз - из 4 точек, и четвертый груз - из 3 точек. Таким образом, имеем 6*5*4*3 = 360 возможных вариантов.

5. При пяти дополнительных грузах мы можем выбрать первый груз из 6 точек, второй груз - из 5 точек, третий груз - из 4 точек, четвертый груз - из 3 точек, и пятый груз - из 2 точек. Таким образом, имеем 6*5*4*3*2 = 720 возможных вариантов.

6. Наконец, при шести дополнительных грузах у нас остается только одна точка, куда мы можем их подвесить, поэтому имеем только один возможный вариант.

Суммируя все возможные варианты, получаем общее число уравновешиваний рычага в данном случае при шести дополнительных грузах:
6 + 30 + 120 + 360 + 720 + 1 = 1237.

Таким образом, существует 1237 возможных вариантов уравновешивания рычага при данном количестве дополнительных грузов (6).