Схемы электрических цепей на рисунке. Определить: Rэкв – эквивалентное сопротивление цепи, Р, U, I, - мощность, напряжение
или силу тока на входе цепи Ui, Ii - токи и напряжения на
всех элементах цепи. В ходе решения выполнить несколько проверок полученных
результатов по законам Кирхгофа.
P-2000Вт U(B)-? I(A)-? R1-60 Ом R2-10 Ом R3-20 Ом R4-40 Ом R5-10 Ом R6-1 Ом R7-20 Ом R8-12 Ом R9-5 Ом R10-10 Ом
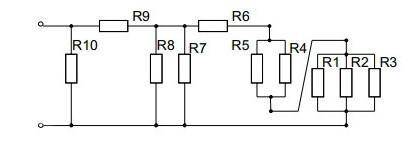
Другие вопросы по теме Физика
Популярные вопросы
- Write type 2 conditionals to match these situations: 1. he spends all his money...
1 - На каких условиях боярин мог получить от князя вотчину? мог ли он ее потерять,...
3 - Составить уравнения реакций превращений: уголь--углекислый газ--угарный газ--цинк--оксид...
2 - Радиус окружности 2 см. найдите длинну окружности...
3 - Подбери синонимы к данным словам. а) личный, священный б) хозяин, владелец...
1 - Сделай буквенную запись слов. про[ч] спло[ш] насте[ш] невмо[ч] наотма[ш] навзни[ч]...
3 - Можете написать краткий отзыв про книгу дикие лебеди (11 )...
3 - укажите лишнее слово 1) родились 2) живут 3) живёте 4) учатся...
3 - Ребенок родился весом 3900. какой вес должен быть у него в 6 месяцев 6 лет 12...
3 - Почему герде удалось найти и кая? сказочник андерсен верит, что добро всегда справится...
3
Давайте начнем с определения эквивалентного сопротивления цепи (Rэкв). Эквивалентное сопротивление можно определить, применяя законы последовательного и параллельного соединения сопротивлений.
Сопротивления R1, R7 и R9 соединены параллельно, поэтому их эквивалентное сопротивление Rp1 можно вычислить с помощью формулы:
1/Rp1 = 1/R1 + 1/R7 + 1/R9
1/Rp1 = 1/60 + 1/20 + 1/5
1/Rp1 = (1/60 + 3/60 + 12/60)
1/Rp1 = 16/60
1/Rp1 = 4/15
Rp1 = 15/4
Rp1 = 3.75 Ом
Теперь сопротивления R3, R5 и R10 соединены последовательно, поэтому их эквивалентное сопротивление Rp2 можно вычислить с помощью формулы:
Rp2 = R3 + R5 + R10
Rp2 = 20 + 10 + 10
Rp2 = 40 Ом
Теперь у нас есть два сопротивления Rp1 и Rp2, которые соединены параллельно. Мы можем вычислить их эквивалентное сопротивление Rэкв с помощью формулы:
1/Rэкв = 1/Rp1 + 1/Rp2
1/Rэкв = 1/3.75 + 1/40
1/Rэкв = (40/3.75 + 3.75/40)
1/Rэкв = 886/75
Rэкв = 75/886
Rэкв ≈ 0.0847 Ом
Теперь перейдем к определению мощности (P), напряжения (U) и силы тока (I) на входе цепи.
Мощность (P) рассчитывается с помощью формулы:
P = U * I
Дано, что мощность P равна 2000 Вт. Предположим, что напряжение (U) равно Ui, а сила тока (I) равна Ii. Тогда
2000 = Ui * Ii
Теперь давайте разобъем цепь на две части для удобства решения:
1. Первая часть цепи состоит из сопротивлений R1 и R2, которые соединены последовательно. Тогда общее сопротивление этой части цепи (Re1) можно найти как сумму R1 и R2:
Re1 = R1 + R2
Re1 = 60 + 10
Re1 = 70 Ом
2. Вторая часть цепи состоит из сопротивлений R3, R4, R5, R6, R7, R8 и R9, которые соединены параллельно. Тогда общее сопротивление этой части цепи (Re2) можно вычислить с помощью формулы:
1/Re2 = 1/R3 + 1/R4 + 1/R5 + 1/R6 + 1/R7 + 1/R8 + 1/R9
1/Re2 = 1/20 + 1/40 + 1/10 + 1/1 + 1/20 + 1/12 + 1/5
1/Re2 = (2/40 + 1/40 + 4/40 + 40/40 + 2/40 + 5/60 + 12/60)
1/Re2 = 42/60
1/Re2 = 7/10
Re2 = 10/7
Re2 ≈ 1.4286 Ом
Теперь у нас есть два сопротивления Re1 и Re2, которые соединены параллельно. Мы можем вычислить их эквивалентное сопротивление Rekv с помощью формулы:
1/Rekv = 1/Re1 + 1/Re2
1/Rekv = 1/70 + 1/1.4286
1/Rekv = (1/70 + 50/7143)
1/Rekv = 5143/500210
Rekv ≈ 0.009757 Ом
Теперь, используя полученное значение эквивалентного сопротивления Rэкв, можем найти напряжение (Ui) и силу тока (Ii) на входе цепи, подставив значения в уравнение о мощности:
2000 = Ui * Ii
Так как Rэкв = 0.0847 Ом, можем выразить силу тока (Ii) как:
Ii = Ui / Rэкв
Подставляя эту формулу в исходное уравнение мощности:
2000 = Ui * (Ui / Rэкв)
Перепишем это уравнение:
2000 = (Ui^2) / Rэкв
Теперь можем выразить напряжение (Ui) через эквивалентное сопротивление (Rэкв) и известную мощность (2000 Вт):
Ui^2 = 2000 * Rэкв
Ui = √(2000 * Rэкв)
Таким образом, напряжение (Ui) на входе цепи равно квадратному корню от произведения мощности (2000 Вт) и эквивалентного сопротивления (Rэкв).
Теперь, зная напряжение (Ui), можем найти силу тока (Ii):
Ii = Ui / Rэкв
Таким образом, сила тока (Ii) на входе цепи равна отношению напряжения (Ui) к эквивалентному сопротивлению (Rэкв).
Теперь, чтобы найти напряжение (U) и силу тока (I) для каждого элемента цепи, применим закон Ома:
U = R * I
1. Для элемента R1:
U1 = R1 * Ii
U1 = 60 * Ii
2. Для элемента R2:
U2 = R2 * Ii
U2 = 10 * Ii
3. Для элемента R3:
U3 = R3 * Ii
U3 = 20 * Ii
4. Для элемента R4:
U4 = R4 * Ii
U4 = 40 * Ii
5. Для элемента R5:
U5 = R5 * Ii
U5 = 10 * Ii
6. Для элемента R6:
U6 = R6 * Ii
U6 = 1 * Ii
7. Для элемента R7:
U7 = R7 * Ii
U7 = 20 * Ii
8. Для элемента R8:
U8 = R8 * Ii
U8 = 12 * Ii
9. Для элемента R9:
U9 = R9 * Ii
U9 = 5 * Ii
10. Для элемента R10:
U10 = R10 * Ii
U10 = 10 * Ii
Таким образом, мы можем найти напряжение (U) и силу тока (I) для каждого элемента цепи, используя ранее найденную силу тока (Ii).
Для проверки полученных результатов по законам Кирхгофа, необходимо применить закон сохранения заряда и закон сохранения энергии. Закон сохранения заряда утверждает, что общая сумма токов, втекающих в узел, равна общей сумме токов, вытекающих из узла. Закон сохранения энергии утверждает, что сумма напряжений в замкнутом контуре равна нулю.
Теперь, подставив найденные значения в уравнения проверки по законам Кирхгофа, можно убедиться, что результаты верны.