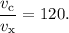Секундна стрілка удвічі довша за хвилинну. Обчислити відношення лінійних швидкостей кінців цих стрілок.
Другие вопросы по теме Физика
Популярные вопросы
- 2x+2y=7 решить складания 3x-2y=5 ...
1 - Скласти з тих слів речення до ть ♥️: Saturday, cleaned, they, the house...
3 - На свой день рождения Петя придумал для друзей такой конкурс: нужно бросить мяч...
3 - Нужен диалог бабушек нужно сегодня...
3 - 3 высказывания о любой книге на ваш выбор...
2 - Написать эти дроби, и придумать к дробям иллюстрацию....
1 - Перевести число восемь в дробь...
2 - Решите очень надо70÷x=20÷2?...
1 - Твір-роздум на тему Хто я?...
2 - Укажіть прості числа які розташовані в натуральному ряді між числами 2 і 12 ...
2
Дано:
Знайти: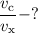
Розв'язання. Довжина кола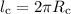 , яке проходить секундна стрілка, за час, що дорівнює одному періоду
, яке проходить секундна стрілка, за час, що дорівнює одному періоду 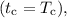 характеризує лінійну швидкість
характеризує лінійну швидкість 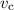 секундної стрілки:
секундної стрілки:
Довжина кола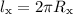 , яке проходить хвилинна стрілка, за час, що дорівнює одному періоду
, яке проходить хвилинна стрілка, за час, що дорівнює одному періоду 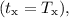 характеризує лінійну швидкість
характеризує лінійну швидкість 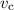 хвилинної стрілки:
хвилинної стрілки:
Оскільки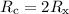 і
і 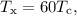 то маємо:
то маємо:
Відповідь: