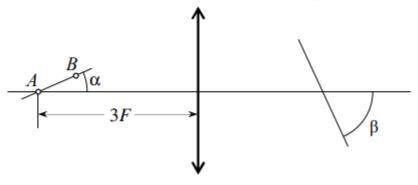
С собирающей линзы получают изображения двух точечных источников А и В, один из которых расположен на главной оптической оси линзы, а другой — на небольшом расстоянии от неё, так что
линия АВ образует с осью угол α = °5 .
Под каким углом β к оптической оси
нужно расположить плоский экран,
чтобы на нём одновременно получались чёткие изображения обоих источников, если источник А находится на
расстоянии 3F от линзы?

Для решения данной задачи нам нужно использовать три основные оптические формулы: формулу тонкой линзы, формулу ловушки лучей и формулу Снеллиуса.

1. Формула тонкой линзы:
1/F = 1/f - 1/d_o
где F - фокусное расстояние, f - фокусное расстояние линзы, d_o - расстояние объекта от линзы.

2. Формула ловушки лучей:
ΔH/H = Δd/d
где ΔH - изменение высоты изображения, H - исходная высота изображения, Δd - изменение расстояния плоскости изображения от линзы, d - исходное расстояние плоскости изображения от линзы.

3. Формула Снеллиуса:
n₁sinθ₁ = n₂sinθ₂
где n₁ и n₂ - показатели преломления среды, sinθ₁ и sinθ₂ - синусы углов падения и преломления соответственно.

Теперь давайте решим задачу:

1. Найдем фокусное расстояние линзы (f):
Из условия задачи мы знаем, что источник А находится на расстоянии 3F от линзы.
Подставим значения в формулу тонкой линзы:
1/F = 1/f - 1/d_o
1/3F = 1/f - 1/3F
1/f = 2/3F
f = 3F/2

2. Найдем угол преломления (θ₁) для луча, проходящего через источник А:
Из геометрии понимаем, что α = θ₁.
Также у нас есть угол преломления (θ₂) для луча, идущего к точке В (луч, идущий от источника В, перпендикулярен оси линзы и, следовательно, не преломляется).
Мы должны найти угол β, под которым нужно разместить плоский экран, чтобы получить чёткие изображения обоих источников. Из геометрии понимаем, что β = θ₂.

3. Найдем изменение расстояния плоскости изображения (Δd) и изменение высоты изображения (ΔH) для луча, проходящего через источник А:
Используем формулу ловушки лучей:
ΔH/H = Δd/d
ΔH/H = f/(d - f) (так как d > f в нашей задаче)
ΔH/H = (3F/2)/(3F/2 - 3F/2)
ΔH/H = 1

4. Найдем показатель преломления среды перед линзой (n₁) и среды после линзы (n₂):
Из условия задачи нам не даны значения показателей преломления, поэтому предположим, что исследуемые лучи находятся в одной среде, например, в воздухе. Таким образом, n₁ = n₂ = 1.

5. Найдем угол преломления (θ₂) для луча, идущего к точке В:
Из формулы Снеллиуса получаем:
n₁sinθ₁ = n₂sinθ₂
1sinα = 1sinθ₂
sinα = sinθ₂
α = θ₂

Мы получили, что α = β = θ₁ = θ₂. Из этого следует, что угол β, под которым нужно разместить плоский экран, чтобы получить чёткие изображения обоих источников, равен α = °5.

Таким образом, чтобы на плоском экране одновременно получились чёткие изображения обоих источников, экран должен быть размещен под углом β = α = °5 к оптической оси.