1. Физика
  2. Решить с дано кто может.

Решить с дано кто может. 1) найдите период и частоту колебания, если маятник совершил 18 колебаний за 15 с. 2) найдите период колебаний маятника , если длина нити подвеса равна 40 см . здесь и ниже g=10м/с^2 3) каким будет период и частота колебаний маятника с длиной нити 10 м . 4) найдите длину нити маятника, совершающего 20 колебаний за 30 c.

uztstdgiDima uztstdgiDima    3   20.05.2019 01:30    2

Ответы
2004тигр2004 2004тигр2004  13.06.2020 07:55

Частота - это число колебаний в единицу времени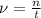 \nu=\frac{n}{t}, где n - число колебаний, t - промежуток времени (с). Вычислим: 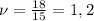\nu=\frac{18}{15}=1,2 Герц.

Период обратен частоте т.е.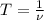 T=\frac{1}{\nu}. Вычислим: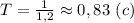 T=\frac{1}{1,2}\approx0,83 \ (c)

 

По формуле математического маятника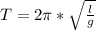 T=2\pi*\sqrt{\frac{l}{g}}, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). В системе СИ: 40 см = 0,4 метра. Подставляем числовые значения и вычисляем: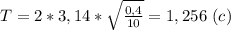 T=2*3,14*\sqrt{\frac{0,4}{10}}=1,256 \ (c)

 

По формуле математического маятника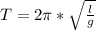 T=2\pi*\sqrt{\frac{l}{g}}, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). Подставляем и вычисляем: период: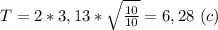 T=2*3,13*\sqrt{\frac{10}{10}}=6,28 \ (c)

Частота следовательно будет равна: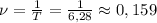 \nu=\frac{1}{T}=\frac{1}{6,28}\approx0,159 Гц

 

Используем две формулы периода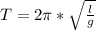 T=2\pi*\sqrt{\frac{l}{g}}, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²) и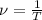 \nu=\frac{1}{T}

Левые части формул равны, следователь и правые части также равны: 

\frac{1}{\nu}=2\pi*\sqrt{\frac{l}{g}}.

Распишем частоту: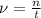 \nu=\frac{n}{t}

\frac{1}{\frac{n}{t}}=2\pi*\sqrt{\frac{l}{g}}

\frac{t}{n}=2\pi*\sqrt{\frac{l}{g}}

n*2\pi*\sqrt{\frac{l}{g}}=t

(n*2\pi*\sqrt{\frac{l}{g}})^2=t^2

n^2*4\pi^2*\frac{l}{g}=t^2

l=\frac{g*t^2}{n^2*4\pi^2}

Подставляем и вычисляем: 

l=\frac{10*30^2}{20^2*4*3,14^2}\approx0,57 \ (_M)

 

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
vovashkaruba vovashkaruba  27.07.2019 08:50
Какой максимальный выигрыш в силе можно получить с гидравлического пресса, площади поршней которого s^1 = 4 см^2 и s^2 = 2 метрам в квадрате? чему будет равен в этом случае модуль...
хочузнать2018 хочузнать2018  27.07.2019 08:50
Практическая по . чем отличаются 2010ne , 2110ne , 2210ne...
elinashovhalova elinashovhalova  27.07.2019 08:50
На проводник длинной 1 м действует сила 0,5h найти магнитную индукцию если ток силой 10а образует угол 30 градусов...
anyutarak03 anyutarak03  27.07.2019 08:50
Какую частоту имеют волны с длиной 1,5 мкм...
880055553555 880055553555  13.09.2019 04:00
Під час конденсації пари відстань між її мі а)збільшується б)зменшується в) залишається незмінною г) збільшується або зменшується (залежно від температури конденсації)...
katevina katevina  13.09.2019 04:00
Определите силу возникающую при растяжении резинового жгута жесткостью 50 ньютон на метр .на 2 см...
Aalina23 Aalina23  13.09.2019 04:00
Під час конденсації пари відстань між її мі а)збільшується б)зменшується в) залишається незмінною г) збільшується або зменшується (залежно від температури конденсації)...
N1ki4 N1ki4  13.09.2019 04:00
На стіні кают-компанії висить годинник, маятник якого коливається з частотою 0,5 гц.скільки коливань здійснить маятник під час подорожі судна з одеси до маріуполя? середня швидкість...
tukva83 tukva83  13.09.2019 04:00
Сколько молекул находится в пустой литровой банке пои при температуре 20°c и нормальным атмомферном давлении 10^5 па.решите...
5Августина5 5Августина5  15.04.2019 22:39
Найти силу тока несамостоятельного разряда, возникающего с ионизатора, который создает 2×106 пар ионов за 1с....

Популярные вопросы