Решить, нужно, . сколько можете (хоть одну). 1.мальчик, стоя на льду, пытается сдвинуть ящик за привязанную к нему веревку. масса ящика 90 кг, масса мальчика 45 кг. коэффициент трения ящика о лед 0,3, а мальчика 0,4. под каким минимальным углом к горизонту мальчик должен тянуть веревку, чтобы сдвинуть ящик? ответ округлить до целого числа градусов. 2.внутри откачанной до глубокого вакуума установки находится герметичный теплоизолированный цилиндрический сосуд, заполненный идеальным одноатомным газом. сосуд закрыт сверху теплонепроницаемым поршнем. газ занимает при этом объем 100 см3. на поршень ставят гирю в 4 раз большей массы, чем масса поршня. найти объем газа в новом положении равновесия. ответ дать в см3 3.мальчик умеет плавать со скоростью 0,6 от скорости течения реки. он хочет переплыть эту реку так, чтобы его как можно меньше снесло вниз по течению. на какое расстояние его снесет, если он будет придерживаться оптимальной стратегии? ширина реки 120 м. 4.марсоход имеет небольшую пушку, которая может стрелять снарядом с одинаковой начальной скоростью под любыми углами к горизонту. если марсоход неподвижен, то максимальная дальность полета оказывается 100 м. какая максимальная дальность будет у снаряда, выпущенного из этой пушки по ходу движения марсохода, идущего горизонтально со скоростью 20 м/с? ускорение свободного падения на марсе считать 4 м/с2. высотой марсохода пренебречь. ответ дать в метрах и округлить до целых. 5.по заснеженной дороге на снегоплавильный пункт с постоянной скоростью 20 м/с едет самосвал груженый снегом. в кузове самосвала имеется дырка, через которую на дорогу дополнительно высыпается снег, причём за одинаковые промежутки времени высыпается одинаковая масса 3 кг/с. вдогонку за самосвалом отправляется снегоуборочный комбайн с бункером. он едет со скоростью v и собирает с дороги весь снег до заполнения бункера. выяснилось, что если бы скорость самосвала была в 3 раза большей, то время заполнения бункера увеличилось бы в 2 раза, при неизменной скорости комбайна. определите линейную плотность снега на заснеженной дороге λ (грамм/м), т.е. сколько грамм приходилось на каждый метр длины дороги до того как по ней проехал самосвал? считать что изначально бункер пустой, его объём меньше объема снега в самосвале и за время заполнения комбайн не догоняет самосвал. потерями пренебречь! (ответ округлите, до ближайшего целого) 6.два бруска массы 4 кг каждый, связанные нитью, соскальзывают с наклонной плоскости с углом α=60 ∘. коэффициент трения нижнего бруска о плоскость 0,2, верхнего 0,3. определите силу натяжения нити. g=10м/с2. 7.через время 4 c скорость брошенного под углом к горизонту тела оказалась перпендикулярна начальной скорости. найдите перемещение тела за это время. сопротивлением среды пренебречь. g=10м/с2.
Другие вопросы по теме Физика
Популярные вопросы
- Рандомные числа от 10 до 300...
3 - у мамы и у попы зичу по25грн разом50 в магазыни купляю продукты на 45грн...
1 - Соотнесите наименование АХОВ и его воздействия на человека....
3 - Нужно найти: Оборотный капитал предприятия...
2 - Появление какого понятия связано с царствованием Ивана IV? ...
1 - довести що для будь-яких значень а вираз -а2+6а-9 набуває тільки від...
2 - Часть 1. Магир отправил Нарнине текстовый файл.Длина текстового сообщения...
1 - 2. Вызначыць трыванне дзеясловаў (3 - закончанае трыванне, H - незакончанае...
2 - Составить таблицу по учебнику 7 класса (все физические понятия разнести...
1 - На современном этапе плауны и хвощи находятся на стадии а)морфологического...
3
Задача №7
1. Введем прямоуголную систему координат следующим образом, полож. нарпавление оси Оу совпадает с направлением начальной скорости тела, а полож. направление оси Ох совпадает с направлением скорости тела через 5 с, то есть перпендикулярно (по усл.)
2. В векторном виде: S(суммарное)=S(по оси Ох)+S(по оси Оу).
Т.к. угол между векторами 90, то S(суммарное) найдем по теореме Пифагора, зная перемещение вдоль оси Ох, и перемещение вдоль оси Оу.
3. Пусть v0 - начальная скорость, v - скорость тела через время t=5с, y - перемещение тела вдоль оси Оу, х - перемещение тела вдоль оси Ох, угол а - угол между вектором v0 и горизонтом, (а также угол между вектором g и осью Ох), тогда:
Oy: 0=v0-g*sin a*t, где t = 5 c, то есть v0=g*sin a*t
Ox: v=0+g* cos a*t, то есть v=g*cos a*t
y=v0*t -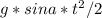 ; так как v0=g*sin a*t, то:
; так как v0=g*sin a*t, то:
y =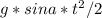
x=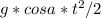
4. s=√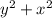
s=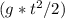 √
√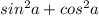 , согласно основному тригонометрическому тождеству выражение под корнем равно 1, следовательно корень равен 1, а значит:
, согласно основному тригонометрическому тождеству выражение под корнем равно 1, следовательно корень равен 1, а значит:
s=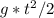
s=10*4*4/2=80(м)
ответ: 80 м