Реши задачу, пошагово выполняя указанные действия и заполняя пропуски. Наибольшая высота подъёма математического маятника массой 318 гв процессе колебаний равна
5,1 см. Определи, какова его наибольшая скорость. При расчётах прими g = 9,8 м/с?
(Все вычисления проводи с точностью до тысячных.)
Шаг 1.
Выразим заданные величины В СИ:
масса маятника:
m — 318 г = 0.381 кг,
наибольшая высота подъёма маятника:
h5,1 см = 0.051
М.
w
Рассмотрим движение данного маятника в двух точках: в точке с наибольшей высотой подъёма
(крайней левой или крайней правой) и в точке равновесия.
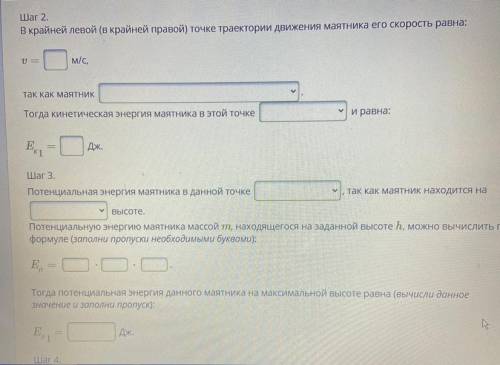
Шаг 2.
В крайней левой (в крайней правой) точке траектории движения маятника его скорость равна:
1
м/с.
так как Маятник

Для решения этой задачи, нам понадобятся уравнения сохранения энергии и закон сохранения механической энергии.

Первым шагом, мы должны выразить заданные величины в Системе Международных единиц (СИ):

- Масса маятника: m = 318 г = 0.318 кг (округляем до тысячных)
- Высота подъема маятника: h = 5,1 см = 0.051 м

Затем мы должны рассмотреть движение маятника в двух точках: наибольшей высоте подъема (крайней левой или крайней правой точке) и в точке равновесия.

В крайней левой (или крайней правой) точке траектории движения маятника его скорость равна 0 м/с. Это происходит потому, что в верхней точке траектории вся кинетическая энергия превращается в потенциальную энергию, и наоборот.

Теперь мы можем использовать уравнение сохранения энергии:

Potencialnaya_energiya = Kineticcheskaya_energiya

mgh = 1/2 * mv^2

где m - масса маятника, g - ускорение свободного падения (примем его равным 9.8 м/с^2), h - высота подъема маятника, v - скорость маятника.

Подставляем известные значения:

0.318 * 9.8 * 0.051 = 1/2 * 0.318 * v^2

Здесь нам известны все значения, кроме v (скорости маятника). Решим это уравнение, чтобы определить v.

Обратите внимание, что у нас есть две неизвестные величины - масса маятника (m) и скорость (v). Но, поскольку задача просит определить наибольшую скорость, мы можем пренебречь массой маятника. Таким образом, упростим уравнение:

9.8 * 0.051 = 1/2 * v^2

Умножаем значение ускорения свободного падения на высоту подъема:

0.5028 = 1/2 * v^2

Умножаем обе стороны уравнения на 2, чтобы избавиться от деления на 1/2:

1.0056 = v^2

Теперь извлекаем квадратный корень из обеих сторон:

v = √1.0056

Округляем до тысячных:

v ≈ 1.003 м/с

Таким образом, наибольшая скорость маятника равна примерно 1.003 м/с.