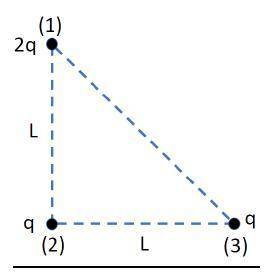
Рассмотрим массив из трех зарядов, показанный на диаграмме. а) Найдите силу заряда (1), вызванную двумя другими зарядами.
б) Вычислите электрическое поле в положении заряда (1), обусловленное двумя другими зарядами.
с) Рассчитайте электрическую потенциальную энергию системы.
Популярные вопросы
- Напишіть будь-ласка невелике повідомлення на тему творчий шлях...
3 - Морфологичиский разбор слова (зимнего)...
1 - Найти площадь фигуры 12 см, 4 см., 4 см, 6 см....
2 - Решите уравнения по ! ! ((2,318-1,118): 4+1,7)х=4,8 ((3,174-2,074):...
2 - Правописание не с причастиями из художественной (выпишите 5 предложений)...
3 - Здраствуйте! ! при повреждении ребер на грудную клетку накладывают...
1 - Ссочинением! (французский язык) по своей подруги маши софи тюрбо...
2 - Для получения хлорида алюминия взяли 54кг.алюминия.какую массу...
1 - 1)найактивніший лужний елемент 2) найактивніший не метал елемент...
1 - Распишите принцип действия водомерного стекла...
1
Дано:
q₁ = 2q
q₂ = q
q₃ = q
r₁₂ = r₂₁ = L
r₂₃ = r₃₂ = L
k
F, E, Wp - ?
Массив из трёх зарядов образует прямоугольный треугольник с равными катетами L (расстояниями r₁₂ и r₂₃). Тогда расстояние r₁₃ (гипотенуза) по правилу Пифагора равно:
r₁₃ = √(r₁₂² + r₂₃²) = √(L² + L²) = √(2L²) = √2*L =>
=> r₁₃ = r₃₁ = √2*L
Но нам будет удобен квадрат расстояния r₁₃(r₃₁):
r₁₃² = r₃₁² = 2L²
Т.к. две стороны треугольника равны, то треугольник является равнобедренным. Тогда углы при основании (r₁₃) равны. Т.к. угол в вершине треугольника (q₂) является прямым, т.е. 90°, то углы при основании равны α = 45°.
а) Теперь найдём силы, с которыми действуют на заряд q₁ заряды q₂ и q₃ (что то же самое - найдём "силу заряда, вызванную двумя другими зарядами"). Все заряды являются положительными, значит действующие между ними кулоновские силы - это силы отталкивания:
F₃₁ = k*(q₁*q₃)/r₃₁² = k*(2q*q)/(2L²) = k*q²/L²
F₂₁ = k*(q₁*q₂)/r₂₁² = k*(2q*q)/L² = k*2q²/L²
Чтобы найти F, надо найти векторную сумму (F₃₁ + F₂₁). Я опущу значок вектора в следующем выражении, но он должен быть над всеми F:
F = F₃₁ + F₂₁
А вот как эта сумма будет выглядеть геометрически (уже без значков):
F = √(F₃₁² + F₂₁² - F₃₁*F₂₁*cos(π - α)) - для нахождения F использована теорема косинусов. На рисунке показано, как получается угол (π - α). Угол между вектором F₂₁ и вектором F₃₁ равен углу α, т.к. этот угол и угол между гипотенузой треугольника и противолежащим катетом являются вертикальными. Угол между продолжением вектора F₂₁ и стороной параллелограмма, равной длине вектора F₃₁, равен углу α, т.к. он и угол между вектором F₂₁ и вектором F₃₁ являются соответственными. Ну а продолжение вектора силы F₂₁ составляет развёрнутый угол в 180° Т.е., π. Тогда угол между стороной параллелограмма, равной длине вектора F₂₁, и стороной параллелограмма, равной длине вектора F₃₁, равен разности развёрнутого угла π и угла α: (π - α). Решаем:
F = √(F₃₁² + F₂₁² - F₃₁*F₂₁*cos(π - α)) - возведём для удобства обе части уравнения в квадрат:
F² = F₃₁² + F₂₁² - F₃₁*F₂₁*cos(π - α) = F₃₁² + F₂₁² - F₃₁*F₂₁*(-cosα) = k²*q⁴/L⁴ + k²*2²q⁴/L⁴ + (k*q²/L²)*(k*2q²/L²)*cosα = k²*q⁴/L⁴ + k²*2²q⁴/L⁴ + cosα*k²*2q⁴/L⁴ = (k²*q⁴/L⁴)*(1 + 4 + 2cosα) = (k²*q⁴/L⁴)*(5 + 2cosα) =>
=> F = (k*q²/L²)*√(5 + 2cosα) - это и есть ответ.
б) Найти электрическое поле - значит найти его напряжённость Е. Напряжённость - это отношение силы Кулона, действующей на заряд, к самому заряду:
E = F/q
Мы уже вычислили результирующую силу, действующую на заряд q₁. Тогда напряжённость равна:
E = F/q₁ = ((k*q²/L²)*√(5 + 2cosα)) : 2q = (k*q²/L²)*(1/2q)*√(5 + 2cosα) =>
=> E = (1/2)*(k*q/L²)*√(5 + 2cosα)