Рассчитай, чему равно ускорение свободного падения на Луне, если масса равна 7,35⋅1022 кг, а радиус — 1737 км.
ответ (округли до сотых)
Другие вопросы по теме Физика
Популярные вопросы
- Каким предстает перед нами петрок через мысли степаниды...
2 - З. раствор, какой концентрации соли никеля нужно пригото- вить, чтобы...
2 - если а(0; 0), в(-2; -2) и с(-5; 1), то ac*cb равно: 18 -18 -12 12...
1 - Нужно по таблице истинности построить временную диаграммуодноразрядного...
3 - Чему равен коэффициент c в уравнении x+y+c=0 если она проходит через...
2 - Менша діагональ правильного шестикутника дорівнює 6 см знайдіть площу...
2 - 10клас тести історія україни 1-10питання40...
3 - Для чого необхідні видозміни органів рослинам? 20 б...
1 - найти частное решение уравнения при заданных условиях y +ksint=0 еслип...
3 - Это линейное диффирициальное уравнение 1-го порядка, высшая . y +y=e^-x...
3
ответ: 1,63 м/с²
Объяснение:
Запишем «Дано»:
M = 7,35*10²² кг
R = 1737 км = 1,737 *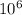 м
м
По закону всемирного тяготения:
Fт =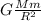 , где
, где
G — гравитационная постоянная (=6,67 *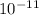 Н*м²/кг²), М — масса планеты, m — масса тела, R — расстояние между телом и планетой (на поверхности планеты — радиус планеты).
Н*м²/кг²), М — масса планеты, m — масса тела, R — расстояние между телом и планетой (на поверхности планеты — радиус планеты).
Также известно, что
Fт = mg, где g — ускорение свободного падения.
То есть
Разделив обе части на m, получим, что
g =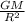
Подставим в эту формулу значения:
g =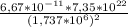 ≈ 16,25 *
≈ 16,25 * 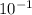 (м/с2) = 1,625 м/с² ≈ 1,63 м/с²
(м/с2) = 1,625 м/с² ≈ 1,63 м/с²