Радиус планеты 2000 км, массы планеты 4 1024 кг. а) Найдите ускорение свободного падения на планете
в) Во сколько раз ускорение на высоте от поверхности, равной двум радиусам планетам, меньше, чем на ее поверхности? Приведите доказательство своего ответа.

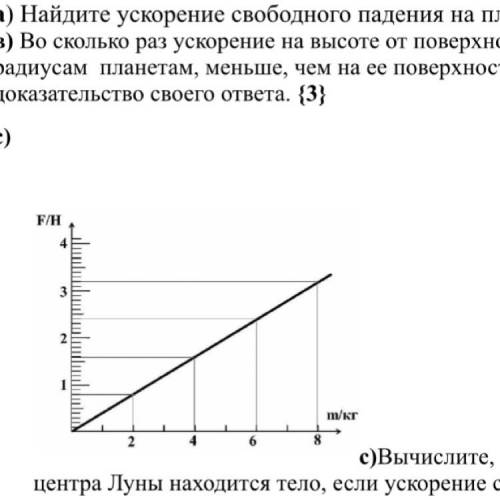
с)Вычислите, на каком расстоянии от центра Луны находится тело, если ускорение свободного падения равно значению из рисунка
СОЧ

Добрый день! Давайте решим вашу задачу по физике.

а) Для того чтобы найти ускорение свободного падения на планете, нам понадобится использовать формулу ускорения свободного падения: g = G * (M / r^2), где g - ускорение свободного падения, G - гравитационная постоянная, M - масса планеты, r - радиус планеты.

Из условия задачи у нас известны значения: M = 4 * 10^24 кг, r = 2000 км = 2000000 м. Гравитационная постоянная G равна 6,67430 * 10^-11 м^3 / (кг * с^2).

Подставим эти значения в формулу и произведем необходимые вычисления:

g = (6,67430 * 10^-11 м^3 / (кг * с^2)) * (4 * 10^24 кг) / (2000000 м)^2.

Выполняя вычисления, получим:

g ≈ 2,5 м/с^2.

Таким образом, ускорение свободного падения на данной планете составляет около 2,5 м/с^2.

б) Теперь нам нужно найти отношение ускорения на высоте, равной двум радиусам планеты, к ускорению на поверхности планеты.

Для этого мы можем использовать формулу ускорения свободного падения на заданной высоте от поверхности планеты: g' = G * (M / (r + h)^2), где g' - ускорение свободного падения на заданной высоте h.

Радиус планеты у нас уже известен - это r = 2000000 м. Если мы задаем высоту h как два радиуса планеты, то h = 2 * r = 2 * 2000000 м = 4000000 м.

Теперь, используя формулу и подставив известные значения, мы можем вычислить значение ускорения на данной высоте:

g' = (6,67430 * 10^-11 м^3 / (кг * с^2)) * (4 * 10^24 кг) / (2000000 м + 4000000 м)^2.

Выполняя вычисления, получим:

g' ≈ 0,694 м/с^2.

Таким образом, ускорение на заданной высоте (равной двум радиусам планеты) составляет примерно 0,694 м/с^2.

Вопрос:

в) Теперь нам нужно вычислить расстояние от центра Луны до тела, если ускорение свободного падения равно 1,76 м/с^2.

На рисунке, который вы привели, дано значение ускорения свободного падения на Луне, а не на заданном расстоянии от центра Луны до тела. Для решения этой задачи, нам понадобится использовать другую формулу.

Формула зависимости ускорения свободного падения от расстояния от центра небесного тела: g' = G * (M / r^2), где g' - ускорение свободного падения на заданном расстоянии r от центра тела.

Мы знаем, что ускорение свободного падения на расстоянии от центра Луны до тела равно 1,76 м/с^2. Масса Луны M и гравитационная постоянная G у нас неизвестны.

Нам не хватает информации, чтобы решить эту задачу. Если у вас есть дополнительные данные, пожалуйста, предоставьте их, и я буду рад помочь вам решить задачу.