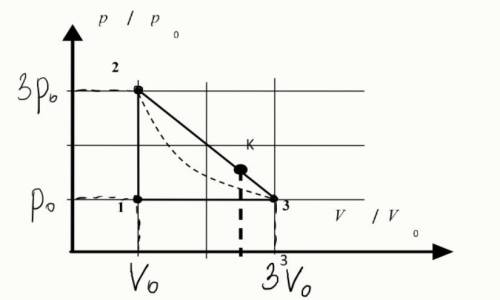
Рабочее тело тепловой машины — ν=3 моль идеального одноатомного газа. Цикл рабочего тела показан на диаграмме в координатах «давление-объём». Пунктиром на диаграмме показана изотерма. Найти максимальную температуру и КПД цикла, если p0=13 атм, а V0=2 л. ответ округлите до целых значений. Максимальная температура?

КПД цикла?

Для решения данной задачи, нам необходимо использовать идеальный газовый закон и знания о работе и энергии в термодинамике.

Давайте разберемся сначала с максимальной температурой. По данной диаграмме видно, что цикл рабочего тела состоит из двух адиабатных процессов и двух изотерм.

Первый адиабатный процесс (процесс AB) - это процесс, в котором не происходит теплообмена с окружающей средой. Это означает, что внешняя работа, совершаемая газом, является равной изменению его внутренней энергии. Формула, которую мы будем использовать для данного процесса, следующая:

W = (γ / (γ-1)) * (p2 *V2 - p1 * V1)

где γ - показатель адиабаты (в данном случае предполагаем, что это одноатомный газ, поэтому γ = 5/3), p1 и p2 - начальное и конечное давление соответственно, V1 и V2 - начальный и конечный объем газа.

Нам неизвестны значения параметров p1, p2, V1 и V2 для процесса AB, потому что они не указаны. Однако, мы можем использовать известные данные, чтобы получить реляцию между этими параметрами.

Из диаграммы видно, что объем газа увеличивается два раза в процессе AB (от V0 до 2V0), а давление снижается изначально до некоторого значения pAB (*на первой изотерме*) и далее до значения p0 (*на второй изотерме*).

p1 = pAB
V1 = V0
V2 = 2V0
p2 = p0

Теперь мы можем использовать эти данные в формуле для адиабатного процесса, чтобы получить внешнюю работу, совершаемую газом в процессе AB.

W_AB = (γ / (γ-1)) * (p0 * 2V0 - pAB * V0)

Известно, что работа в процессе AB равна нулю (так как на диаграмме это фигура на одной горизонтальной линии), поэтому уравнение принимает следующий вид:

0 = (γ / (γ-1)) * (p0 * 2V0 - pAB * V0)

Отсюда мы можем выразить значение pAB:

pAB = (γ / (γ / (γ-1))) * p0 * 2

Аналогичным образом можно рассчитать давление на второй изотерме и получить значение p0:

p0 = (γ / (γ / (γ-1))) * pAB / 2

Теперь, поскольку нам известны значения p0 и pAB, мы можем рассчитать давление на противоположной стороне (точке D), чтобы узнать конечный объем V3:

V3 = V2 * (p2 / p3)

где p3 - давление на точке D. Учитывая, что точка D находится на нижней адиабате (процесс CD), мы можем использовать формулу для адиабатного процесса:

W_CD = (γ / (γ-1)) * (p4 * V4 - p3 * V3)

где W_CD - работа совершаемая газом в процессе CD, p4 и V4 - значения давления и объема на точке C, p3 и V3 - значения давления и объема на точке D.

Мы можем снова заметить, что работа в процессе CD равна нулю (так как на диаграмме это фигура на одной горизонтальной линии), поэтому уравнение принимает следующий вид:

0 = (γ / (γ-1)) * (p4 * V4 - p3 * V3)

Мы знаем, что расстояние между точками C и D равно V3-V4, и поскольку процесс нарисован пунктиром на диаграмме, мы можем сделать предположение, что график этого процесса является изотермическим и получить значение p3:

p3 = (p4 * V4) / V3

В итоге мы можем рассчитать давление на точке D и использовать это значение, чтобы найти конечный объем V3.

Теперь у нас есть все необходимая информация для расчета КПД цикла.

КПД цикла определяется формулой:

КПД = 1 - (Q2 / Q1)

где Q1 - тепло, полученное рабочим телом на горячей стороне (на исотермическом процессе AB), Q2 - тепло, отдаваемое рабочим телом на холодной стороне (на исотермическом процессе CD).

Мы можем использовать формулу для расчета максимальной температуры для определения Q1. Максимальная температура достигается на точке B и определяется следующим выражением:

Tmax = (p0 * V0) / (ν * R)

где R - универсальная газовая постоянная.

Тогда величина Q1 будет следующей:

Q1 = n * R * Tmax * ln(V2 / V1)

где n - количество вещества рабочего тела (в данном случае ν = 3 моль).

Учитывая, что процесс AB является изотермическим, мы можем использовать следующую формулу для расчета Q2:

Q2 = n * R * Т * ln(V3 / V4)

где T - температура на тепловой изотерме (для процесса CD выбирается минимальная температура из всех температур цикла, она будет равна p3 * V3 / (ν * R)).

Теперь, имея значения Q1 и Q2, мы можем подставить их в формулу для КПД цикла и рассчитать его значение.

Надеюсь, что данное пошаговое решение поможет вам лучше понять задачу и получить нужные результаты. Если у вас возникнут вопросы, не стесняйтесь задавать их.