Проводящий стержень, масса единицы длины которого 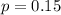
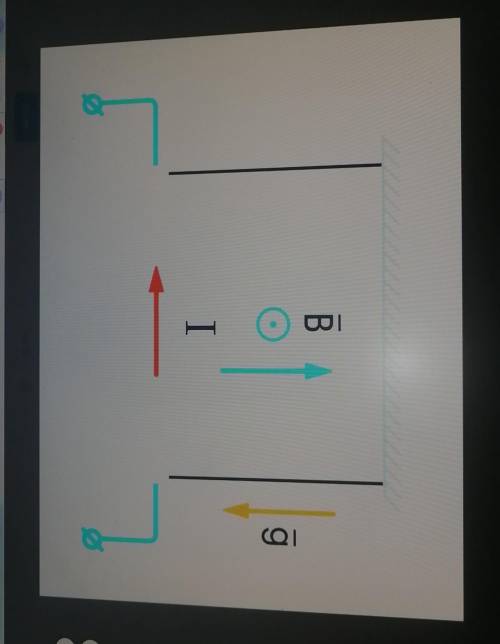
кг/м, подвешен на двух одинаковых непроводящих нитях и помещён в однородное вертикальное магнитное поле, перпендикулярное стержню, как показано на рисунке. По стерженю пропускают электрический ток, в результате чего он занимает новое положение равновесия, в котором нити отклоняются от вертикали. При каком значении силы тока I через проводник нити образуют с вертикалью угол
градусов? Индукция магнитного поля B = 1 Тл, ускорение свободного падения g = 10 м/с в квадрате. ответ вырази в амперах.
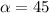
Другие вопросы по теме Физика
Популярные вопросы
- Скорость лодки 18 км/ч. скорость течения реки - 2 км/ч. какое расстояние...
3 - Найдите корни уравнения 5.9x + 2.9x= 27.28...
2 - 1.особенности рельефа мексики(общий характер поверхности,основные формы...
1 - Придумай и запиши примеры существительных по грамматическим признакам...
3 - Сочинение по теме человек и мир природы в (произведение по выбору учащегося)...
3 - Підскажіть будь ласка формули алюмінію міді соди...
2 - Расстояние между 567 км два автомобиля движутся навстречу друг другу...
2 - Найдите сумму площадей всех стен комнаты,если длина комнаты равна 7,2м,ширина5,1м,а...
3 - Найдите длину отрезка ab (в еденичных отрезках) если 1)а(-3)и в(2) 2)а(-5)и...
2 - Масы дыни 3кг а маса арбуза в полтора больше чему равна маса арбуза...
3
Когда ток начинает проходить через стержень, на него начинает действовать магнитная сила, возникающая в результате взаимодействия магнитного поля B и тока I. Эта сила будет направлена перпендикулярно и к полю и к току и в задаче указано, что она перпендикулярна стержню, то есть направлена к центру окружности, образованной нитями. Для нахождения значения силы тока, при котором нити образуют угол a с вертикалью, необходимо найти такое значение тока, при котором сила магнитного поля компенсирует вес стержня и создает равновесие системы.
Разложим магнитную силу Fм по вертикальной и горизонтальной составляющим. Горизонтальная компонента Fгориз будет равна силе натяжения нити, которая направлена к центру окружности и создает угол a с вертикалью. Вертикальная компонента Fверт будет равна весу стержня m*g.
Теперь посмотрим на силы, действующие на нить. Если стержень находится в положении равновесия, натяжение нити направлено по касательной к окружности, а значит, оно будет создавать центростремительное ускорение ac. Это ускорение будет представлять собой горизонтальную компоненту равнодействующей силы T (натяжения нити) по массе единицы длины стержня. Так как масса единицы длины стержня равна p = 0,15 кг/м, то m = p*L, где L - длина стержня. Таким образом, формула для центростремительного ускорения примет вид ac = T/m = T/(p*L).
Рассмотрим теперь моменты сил, действующих на стержень от магнитного поля и от натяжения нити. Момент магнитной силы Mm будет равен произведению магнитной силы Fм на плечо L*sin(a), где а - угол, образованный нитью и вертикалью. Момент силы натяжения Mn будет равен произведению натяжения T на плечо L*cos(a). Для создания равновесия моменты сил должны быть равны, т.е. Mm = Mn.
Подставим значения силы магнитного поля Fм = B*I*L*sin(a) и силы натяжения T = Fгориз = m*ac = p*L*ac в уравнение моментов сил и найдем неизвестное значение силы тока I:
B*I*L*sin(a) = p*L*cos(a)*L*sin(a).
Упростим выражение, сократив L и sin(a):
B*I*sin(a) = p*cos(a).
Выразим неизвестную силу тока I:
I = (p*cos(a))/(B*sin(a)).
Подставим значения величин:
I = (0,15*0,707)/(1*0,707) = 0,15 А.
Таким образом, чтобы нити образовывали угол 45 градусов с вертикалью, сила тока должна быть равна 0,15 А.