ПРАКТИЧЕСКАЯ РАБОТА 2 11Вариант брать значения из этого варианта

ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ КОНДЕНСАТОРА
Цель работы: уяснить влияние физических параметров плоского конден­сатора на его электрическую емкость.
Порядок выполнения работы
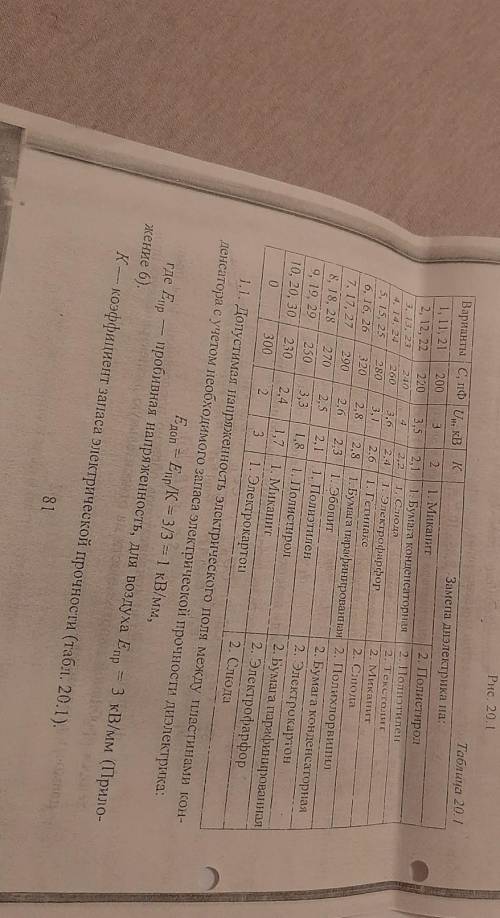
1. Определить площадь S пластин (обкладок) и расстояние между ними d для воздушного конденсатора (рис. 20.1) емкостью С, рассчитанного на работу при номинальном напряжении Uн. При этом должен быть обеспечен запас электрической прочности К (табл. 20.1).
 

1.1. Допустимая напряженность электрического ноля между пластинами кон­денсатора с учетом необходимого запаса электрической прочности диэлектрика:
Eдоп = Eпр/К = 3/3 = 1 кВ/мм,
где Епр — пробивная напряженность, для воздуха Епр = 3 кВ/мм (Прило­жение 6).
К— коэффициент запаса электрической прочности (табл. 20.1).
1.2. Расстояние между пластинами конденсатора:
d = Uн/Eдоп = 2/1=2 мм.
1.3. Определить площадь пластин конденсатора. Так как С = εа S/d, то:
S= Cd/εа = 300 • 10-12 • 2 • 10-3/8,85 • 10-12 = 67,8 • 10-3 м2 = 678 см2,
где εа — абсолютная диэлектрическая проницаемость, для воздуха εа = ε0 = 8,85 • 10-12 Ф/м.
2. Определить, как изменятся размеры конденсатора той же емкости, если в качестве диэлектрика использовать другой, согласно заданию (в варианте «0» электрокартон: ε = 4; Eпр = 9 кВ/мм), с тем же запасом прочности.
2.1. Допустимая напряженность электрического поля конденсатора с элек­трокартоном
Eдоп = Епр/К = 9/3 = 3 кВ/мм.
2.2. Расстояние между пластинами конденсатора (толщина электрокартона)
d = Uн/Eдоп = 2/3 = 0,67 мм.
2.3. Площадь пластин конденсатора
S= 300 • 10-12 • 0,67 • 10-3/4 • 8,85 • 10-12 = 5,65 • 10-3 м2 = 56,5 см2.
Таким образом, у конденсатора той же емкости с электрокартоном в каче­стве диэлектрика размеры уменьшились: d в 3 раза, S в 12 раз.
2.4. Следует обратить внимание на соотношение размеров двух плоских конденсаторов одинаковой емкости с разными диэлектриками:

d2 = d1 * Епр1/Епр2,
т.е. расстояния между пластинами конденсаторов обратно пропорциональ­ны электрической прочности их диэлектриков (пробивной напряженности Eпр).

S2=S1Eпр1ε1/(Eпр2ε2)
т.е. площади пластин конденсаторов обратно пропорциональны произве­дениям пробивной напряженности на относительную диэлектрическую прони­цаемость диэлектриков.
Пользуясь этим соотношением, определить размеры конденсатора с изме­ненным диэлектриком:
d = d1Eпр1/Eпр2 = 2 • 3/9 = 0,67 мм;
S=S1Eпр1 ε1 /(Eпр2ε2) = 678 • 3 • 1/(9 • 4) = 56,5 см2.
Размеры полнились такие же, как в п. 2.3.
3. Определить, как изменится емкость конденсатора, размеры которого определены в п. 1, если промежуток между пластинами заполнить другим диэлектриком (в примере — слюда), т.е. d = 2 мм; S = 67,8 • 10 -3 м2; ε = 6,5; εа = 6,5 • 8,85 • 10-12 = 57,52 • 10-12 Ф/м.
3.1. Емкость конденсатора со слюдой
С = εaS/d = 57,52 • 10-12 • 67,8 • 10-3/2 • 10-3 = 1950 • 10-12 = 1950 пФ.
При замене воздуха в качестве диэлектрика на слюду емкость конденсато­ра увеличилась в 6,5 раз, т.е. во столько, во сколько диэлектрическая проницае­мость данного диэлектрика больше проницаемости воздуха.
3.2. Запас электрической прочности такого конденсатора при заданном UH

К = Епр/Ен = 80/1 = 80,
где Eпр — пробивная напряженность (электрическая прочность) слюды, Епр = 80 кВ/мм (Приложение 6);
Ен— напряженность электрического поля конденсатора при номинальном напряжении Ен = Uн/d = 2/2= 1 кВ/мм.
Выводы: пояснить, что такое электрическая емкость конденсатора; ее за­висимость от физических параметров конденсатора; электрическая прочность​

kidz123    3   29.04.2021 17:40    71