Постоянная распада изотопа Pb 210 82 равна 10^-9 с. Какая доля исходного количества образца этого изотопа распадется за три года?
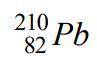
Другие вопросы по теме Физика
Популярные вопросы
- Подсчитать количество нечетных элементов в одномерном массиве...
2 - Решите (3х+1)*(5-2х)+6х(в квадратете)=5...
1 - Напишите пожелания на день матери (только в словах) ....
1 - Вцилиндре под поршнем находится кислород. поршень начинают вдвигать...
1 - Вкувшине было 12 стаканов молока. на кашу пошло 5 стаканов молока,...
3 - Из данных ниже имен сущ выберите такие,которыесочетаютсяс прилагательным...
2 - Высота,опущенная из вершины тупого угла равнобедренной трапеции,делит...
3 - Автор стихотвореня (отрывок) лучше б снег да вьюгу встретить грудью...
3 - Уберите 1-2 буквы что бы получить другое слово волк- кобра-...
3 - 4класс.длина огорода прямоугольной формы 80 м,ширина 35 м . овощями...
2
Задача говорит о распаде изотопа Pb 210 82, у которого постоянная распада равна 10^-9 с. Нам нужно найти долю исходного количества образца этого изотопа, которая распадется за три года.
Для решения этой задачи мы можем использовать радиоактивное распадное уравнение. По этому уравнению, количество оставшегося изотопа в какой-то момент времени (N) равно исходному количеству изотопа (N0) умноженному на экспоненту отрицательной постоянной распада (λ) умноженной на время (t):
N = N0 * e^(-λt)
Где, e - основание натурального логарифма (e=2.71828), λ - постоянная распада, t - время.
Мы знаем, что постоянная распада равна 10^-9 с, а нам нужно найти долю исходного количества, которая распадется за три года.
Исходя из этого, давайте приступим к решению задачи.
Шаг 1: Найдем величину λ, используя данную постоянную распада. Постоянная распада (λ) равна 10^-9 с.
Шаг 2: Переведем время распада из лет в секунды. Мы знаем, что 1 год = 365 дней = 24 часа = 60 минут = 60 секунд. Таким образом, 3 года = 3 * 365 * 24 * 60 * 60 секунд.
Шаг 3: Подставим значения в радиоактивное распадное уравнение:
N = N0 * e^(-λt)
где N - количество оставшегося изотопа, N0 - исходное количество изотопа, λ - постоянная распада, t - время.
Шаг 4: Подставим известные значения: λ = 10^-9 с, t = 3 * 365 * 24 * 60 * 60 секунд.
Шаг 5: Вычислим исходное количество изотопа (N0), которое нужно найти. Для этого перенесем N0 на одну сторону уравнения и возьмем натуральный логарифм от обеих частей уравнения:
N/N0 = e^(-λt)
N0 = N / e^(-λt)
Шаг 6: Подставим значения N, λ и t, которые мы уже нашли, и вычислим N0 (исходное количество изотопа, которое распадется за три года).
Шаг 7: Найдем долю исходного количества образца этого изотопа, которая распадется за три года. Мы можем использовать следующую формулу:
Доля = (N0 - N) / N0
где N0 - исходное количество изотопа, N - количество оставшегося изотопа.
Итак, если выполнить все эти шаги, мы сможем найти искомую долю исходного количества образца изотопа Pb 210 82, которая распадется за три года.